Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Hai tam giác vuông AHD và CKD có:
AD = CB (gt)
= 
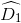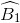(so le trong)
Nên ∆AHD = ∆CKB (cạnh huyền, góc nhọn)
Suy ra AH = CK
Tứ giác AHCK có AH Vuông góc với DB và CK cũng vuông góc với DB. Nên AH // CK, Mà theo chứng mình trên AH = CK nên là hình bình hành,
b) Xét hình bình hành AHCK, trung điểm O của đường chéo của hình bình hành). Do đó ba điểm A, O, C thẳng hàng.
Tham khảo thôi!
a) Hai tam giác vuông AHD và CKD có:
AD = CB (gt)
\(\widehat{D_1}\) = \(\widehat{B_1}\) (so le trong)
Nên ∆AHD = ∆CKB (cạnh huyền, góc nhọn)
Suy ra AH = CK
Tứ giác AHCK có AH Vuông góc với DB và CK cũng vuông góc với DB. Nên AH // CK, Mà theo chứng mình trên AH = CK nên là hình bình hành,
b) Xét hình bình hành AHCK, trung điểm O của đường chéo của hình bình hành). Do đó ba điểm A, O, C thẳng hàng.
b) Xét hai tam giác vuông AHD và CKB có:
AD=BC
góc ADB=góc DBC (so le trong).
=> tam giác AHD=tam giác CKB (ch-gn)
=> BH=CK( hai cạnh tương ứng)
Lấy M trung điểm BD , nên MD=MB => MD-DH=MB-BK=> MH=MK, nên M Trung điểm HK
Vì ABCD là hình bình hành nên AC cắt BD tại trung điểm M.
Hay M là Trung điểm AC, mà M trung điểm HK.
Nên AKCH là hình bình hành.
bạn tự phác hình ra nhé
a) Xét tứ giác AHCK có AH _|_ BD và CK _|_ BD => AH // CK
xét tam giác AHD và tam giác CKB có:
\(\widehat{H}=\widehat{K}=90^o\)
AD=BC
\(\widehat{ADH}=\widehat{CBK}\)
\(\Rightarrow\Delta AHD=\Delta CKB\)(cạnh huyền-góc nhọn)
=> AH=CK
vậy tứ giác AHCK là hình bình hành
b) xét hình bình hàng AHCK, trung điểm O của đường chéo HK cũng là trung điểm của đường chéo AC (tính chất đường chéo của hình bình hành) do đó 3 điểm A,O,C thẳng hàng (đpcm)
a) Xét ΔAHD và ΔCKB có:
AD = BC (gt)
góc ADB = góc DBC ( SLT).
=> ΔAHD = ΔCKB (cạnh huyền- góc nhọn)
=> BH = CK( hai cạnh tương ứng)
Lấy M trung điểm BD
=> MD = MB
=> MD - DH = MB - BK
=> MH = MK (vì M Trung điểm HK)
Vì ABCD là hình bình hành nên AC cắt BD tại trung điểm M.
Hoặc M là Trung điểm AC và M trung điểm HK.
=> Tứ giác AKCH là hình bình hành (đpcm)
Do P là trung điểm của BC nên :
=) CP=BP=\(\frac{BC}{2}\)
Do Q là trung điểm của AD nên:
=) AQ=QD=\(\frac{A\text{D}}{2}\)
Mà AD=BC (Tính chất hình bình hành)
=) BP=AQ=PC=QD (1)
Mà 2 cạch AP và BP lại song song với nhau (2)
TỪ (1)và(2) =) Tứ giác ABPQ là hình bình hành
b) Do AD=2AB =) AB =\(\frac{A\text{D}}{2}\)=) AQ=AB
Mà AQ=BP (Tính chất hình bình hành)
Và AB=PQ (Tính chất hình bình hành)
=) AB=BP=PQ=AQ
=) Tứ giác ABPQ là hình thoi
=) 2 đường chéo AP và BQ vuông góc với nhau
Hay AP \(\perp\)BQ
c) Do tứ giác ABPQ là hình bình hành nên =) \(\widehat{A}\) =\(\widehat{P}\)= \(60^0\)
Xét tam giác BPQ có :
QP=PB (chứng minh trên )
\(\widehat{P}\)= \(60^0\)
=) Tam giác BPQ là tam giác đều
=) \(\widehat{B}\) =\(60^0\) (1)
Mà \(\widehat{A}\) =\(\widehat{C}\)=\(60^0\)(Do ABCD là hình bình hành ) (2)
Và QP lại song song với BC =) BQDC là hình thang (3)
Tu (1) ;(2) va (3) =) BQDC là hình thang cân
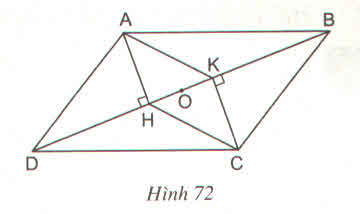
a)+ ABCD là hình bình hành
⇒ AD // BC và AD = BC.
⇒ ∠ADH = ∠CBK (Hai góc so le trong).
Hai tam giác vuông AHD và CKB có:
AD = BC
∠ADH = ∠CBK
⇒ ΔAHD = ΔCKB (cạnh huyền, góc nhọn)
⇒ AH = CK
+ AH ⊥ BD; CK ⊥ BD ⇒ AH // CK
Tứ giác AHCK có AH // CK, AH = CK nên là hình bình hành.
b) Hình bình hành AHCK có O là trung điểm HK
⇒ O = AC ∩ HK ⇒ A, C, O thẳng hàng.