Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

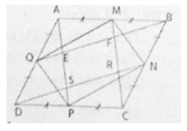
a) Ta có AB // CD (gt)
Suy ra AM // CP (1)
Lại có AM = AB/2; CP = CD/2 (2)
Từ (1) và (2) suy ra AMCP là hình bình hành
Suy ra AP // CM hay ES // FR.
Tương tự ta cũng chứng minh được tứ giác BQDN là hình bình hành nên BQ // DN. Suy ra EF // RS.
Vậy tứ giác EFRS là hình bình hành
b) Đặt PS = x. Suy ra CR = 2x (tính chất đường trung bình)
Từ đó suy ra RF = ES = AE = 2x
Suy ra: ES = 2AP/5 => SEFRS = 2SAMCP/5
Vì SAMCP = SABCD/2 nên SEFRS = SABCD/2

Cô hướng dẫn thôi nhé :)
a. AMCN là hình thoi vì có AN//CM; AN = CM và \(AC\perp MN\)
b. Ta có góc DCB = 120 nên DNMC là hình thoi hay NM = MC = MB. Vậy tam giác NCB vuông tại N.
c. QNPM là hình chữ nhật : NP//QM, NQ//PM, NQ vuông góc PM.
Thấy ngay \(\frac{S_{NQM}}{S_{NMCD}}=\frac{S_{NMP}}{S_{ABMN}}=\frac{1}{4}\Rightarrow\frac{S_{NPMQ}}{S_{ABCD}}=\frac{1}{4}\)
d. Ta tính được DC , từ đó suy ra \(NC=DC\)
\(NB=2DQ=2\sqrt{DC^2-QC^2}\)
Tự vẽ hình nhé, cô sẽ hướng dẫn :)
b. Xét tứ giác DQBN có DQ song song và bằng BN nên đó là hình bình hành. Vậy QB//DN.
Từ đó suy ra được GHKI là hình bình hành hay KH = GI.
Lại có QG và KN là các đường trung bình nên AG = GI = HK = KC.
Tương tự MH cũng là đường trung bình nên AG = 2 MH. Vậy HK = KC =2 MH hay MC = 5 MH.
c. Lập tỉ số diện tích bằng cách dựa vào các tỉ số giữa cạnh đáy là chiều cao của các hình.
Ta có \(\frac{S_{CKN}}{S_{CMB}}=\frac{2}{5}.\frac{1}{2}=\frac{1}{5}\)
Mà \(\frac{S_{CMB}}{S_{ABCD}}=\frac{1}{2}.\frac{1}{2}=\frac{1}{4}\) , vì vậy \(\frac{S_{KCN}}{S_{ABCD}}=\frac{1}{5}.\frac{1}{4}=\frac{1}{20}\)
c. Ta thấy \(\frac{S_{KCN}}{S_{MBC}}=\frac{KC}{MC}.\frac{d\left(B,MC\right)}{d\left(N,MC\right)}=\frac{2}{5}.\frac{1}{2}=\frac{1}{5}\)
Với d(B,MC) là độ dài chiều cao kẻ từ B xuống MC.