Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ hình vẽ ta thấy: S, R là hai trung điểm của hai đoạn thẳng trong tam giác nên NS và MR là hai đường trung tuyến.
G là giao của hai đường trung tuyến nên G là trọng tâm của ΔMNS, do đó ta có thể điền:
a/ MG =\(\dfrac{2}{3}\) MR , GR=\(\dfrac{1}{3}\) MR , GR=\(\dfrac{1}{2}\) MG
b/NS= \(\dfrac{3}{2}\) NG, NS =\(\dfrac{3}{1}\) GS, NG= \(\dfrac{2}{1}\) GS

gọi đa thức cần diền vào chỗ (...) là a
`=>11x^2y-a=15x^2y+1`
`=>a=11x^2y-15x^2y-1`
`=>a=-1-4x^2y`
Vậy đa thức cần điền là `-1-4x^2`y

a) \(\sqrt{121}=11\)
\(\sqrt{12321}=111\)
\(\sqrt{1234321}=1111\)
b) \(\sqrt{123454321}=11111\)
\(\sqrt{12345654321}=111111\)
\(\sqrt{1234567654321}=1111111\)

a) \(\left|a+b\right|\le\left|a\right|+\left|b\right|\)
b) \(\left|a-b\right|\ge\left|a\right|-\left|b\right|\) với \(\left|a\right|\ge\left|b\right|\)
c) \(\left|ab\right|\le\left|a\right|.\left|b\right|\)
d) \(\left|\dfrac{a}{b}\right|\le\dfrac{\left|a\right|}{\left|b\right|}\)

a) \(\sqrt{1}=1\)
\(\sqrt{1+2+1}=2\)
\(\sqrt{1+2+3+2+1}=3\)
b) \(\sqrt{1+2+3+4+3+2+1}=4\)
\(\sqrt{1+2+3+4+5+4+3+2+1}=5\)
\(\sqrt{1+2+3+4+5+6+5+4+3+2+1}=6\)

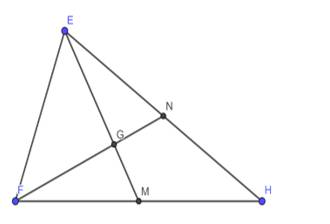
\(\begin{array}{l}EG = \dfrac{2}{3}EM;\,\,\,GM = \dfrac{1}{3}EM;\,\,\,\,GM = \dfrac{1}{2}EG\\FG = 2GN;\,\,\,\,\,FN = 3GN;\,\,\,\,\,\,\,FN = \dfrac{3}{2}FG\end{array}\)
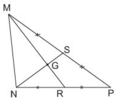
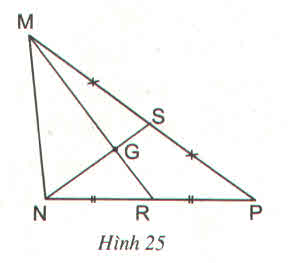


Hình vẽ cho ta biết hai đường trung tuyến MR và NS cắt nhau tại G nên G là trọng tâm của tam giác MNP
Vì vậy ta điền số như sau:
- Ta chứng minh:
G là trọng tâm của tam giác MNP và MR và NS là hai đường trung tuyến.
Nên theo tính chất đường trung tuyến ta có
Ta có