Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Với `m=1`, ta có HPT: \(\left\{{}\begin{matrix}x+2y=18\\x-y=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y=-6\\3y=24\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=8\end{matrix}\right.\)
b. Theo đề bài `=>` \(\left\{{}\begin{matrix}mx+2y=18\\x-y=-6\\2x+y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}mx+2y=18\\x=1\\y=7\end{matrix}\right.\)
`=> m=4`

a)
Khi m = 1, ta có:
{ x+2y=1+3
2x-3y=1
=> { x+2y=4
2x-3y=1
=> { 2x+4y=8
2x-3y=1
=> { x+2y=4
2x-3y-2x-4y=1-8
=> { x=4-2y
-7y = -7
=> { x = 2
y = 1
Vậy khi m = 1 thì hệ phương trình có cặp nghệm
(x; y) = (2;1)
a) Thay m=1 vào HPT ta có:
\(\left\{{}\begin{matrix}x+2y=4\\2x-3y=1\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}2x+4y=8\\2x-3y=1\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}2x+4y=8\\7y=7\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Vậy HPT có nghiệm (x;y)= (2;1)

a) Thay m=1 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}x+2y=4\\2x-3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+4y=8\\2x-3y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7y=7\\x+2y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=4-2y=4-2=2\end{matrix}\right.\)
Vậy: Khi m=1 thì hệ phương trình có nghiệm duy nhất là (x,y)=(2;1)
b) Ta có: \(\left\{{}\begin{matrix}x+2y=m+3\\2x-3y=m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m+3-2y\\2\left(m+3-2y\right)-3y=m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=m+3-2y\\2m+6-4y-3y-m=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m+3-2y\\-7y+m+6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=m+3-2y\\-7y=-m-6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m+3-2y\\y=\dfrac{m+6}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=m+3-2\cdot\dfrac{m+6}{7}\\y=\dfrac{m+6}{7}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m+3-\dfrac{2m+12}{7}\\y=\dfrac{m+6}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{7m+21-2m-12}{7}=\dfrac{5m+9}{7}\\y=\dfrac{m+6}{7}\end{matrix}\right.\)
Để hệ phương trình có nghiệm duy nhất thỏa mãn x+y=3 thì \(\dfrac{5m+9}{7}+\dfrac{m+6}{7}=3\)
\(\Leftrightarrow6m+15=21\)
\(\Leftrightarrow6m=6\)
hay m=1
Vậy: Khi m=1 thì hệ phương trình có nghiệm duy nhất thỏa mãn x+y=3
a/ Thay \(m=1\) vào hpt ta có :
\(\left\{{}\begin{matrix}x+2y=4\\2x-3y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Vậy...
b/ Ta có :
\(\left\{{}\begin{matrix}x+2y=m+3\\2x-3y=m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m+3}{2y}\\\dfrac{2\left(m+3\right)}{2y}-3y=m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m+3}{2y}\\\dfrac{m+3}{y}-3y=m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m+3}{2y}\\m-3y^2+3=my\end{matrix}\right.\)

a: Khi m=3 thì hệ phương trình sẽ là:
\(\left\{{}\begin{matrix}3x-y=2\\2x+3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x-3y=6\\2x+3y=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}11x=11\\3x-y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3x-2=3-2=1\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}mx-y=2\\2x+my=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\2x+m\left(mx-2\right)=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=mx-2\\x\left(m^2+2\right)=5+2m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\x=\dfrac{2m+5}{m^2+2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{2m^2+5m}{m^2+2}-2=\dfrac{2m^2+5m-2m^2-4}{m^2+2}=\dfrac{5m-4}{m^2+2}\\x=\dfrac{2m+5}{m^2+2}\end{matrix}\right.\)
\(x+y=1-\dfrac{m^2}{m^2+2}\)
=>\(\dfrac{5m-4+2m+5}{m^2+2}=\dfrac{m^2+2-m^2}{m^2+2}=\dfrac{2}{m^2+2}\)
=>7m+1=2
=>7m=1
=>\(m=\dfrac{1}{7}\)

a: Thay m=-2 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}x-2y=-2+1=-1\\-2x+y=3\cdot\left(-2\right)-1=-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-4y=-2\\-2x+y=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3y=-9\\x-2y=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=3\\x=2y-1=2\cdot3-1=5\end{matrix}\right.\)
b: Để hệ có nghiệm duy nhất thì \(\dfrac{1}{m}\ne\dfrac{m}{1}\)
=>\(m^2\ne1\)
=>\(m\notin\left\{1;-1\right\}\)
\(\left\{{}\begin{matrix}x+my=m+1\\mx+y=3m-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=m+1-my\\m\left(m+1-my\right)+y=3m-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=m+1-my\\m^2+m-m^2y+y=3m-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=m+1-my\\y\left(-m^2+1\right)=3m-1-m^2-m=-m^2+2m-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=m+1-my\\y\left(m-1\right)\left(m+1\right)=\left(m-1\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{m-1}{m+1}\\x=m+1-m\cdot\dfrac{m-1}{m+1}=\left(m+1\right)-\dfrac{m^2-m}{m+1}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{m-1}{m+1}\\x=\dfrac{m^2+2m+1-m^2+m}{m+1}=\dfrac{3m+1}{m+1}\end{matrix}\right.\)
\(x^2-y^2=4\)
=>\(\dfrac{\left(3m+1\right)^2-\left(m-1\right)^2}{\left(m+1\right)^2}=4\)
=>\(\dfrac{9m^2+6m+1-m^2+2m+1}{\left(m+1\right)^2}=4\)
=>\(8m^2+8m+2=4\left(m+1\right)^2\)
=>\(8m^2+8m+2-4m^2-8m-4=0\)
=>\(4m^2-2=0\)
=>\(m^2=\dfrac{1}{2}\)
=>\(m=\pm\dfrac{1}{\sqrt{2}}\)
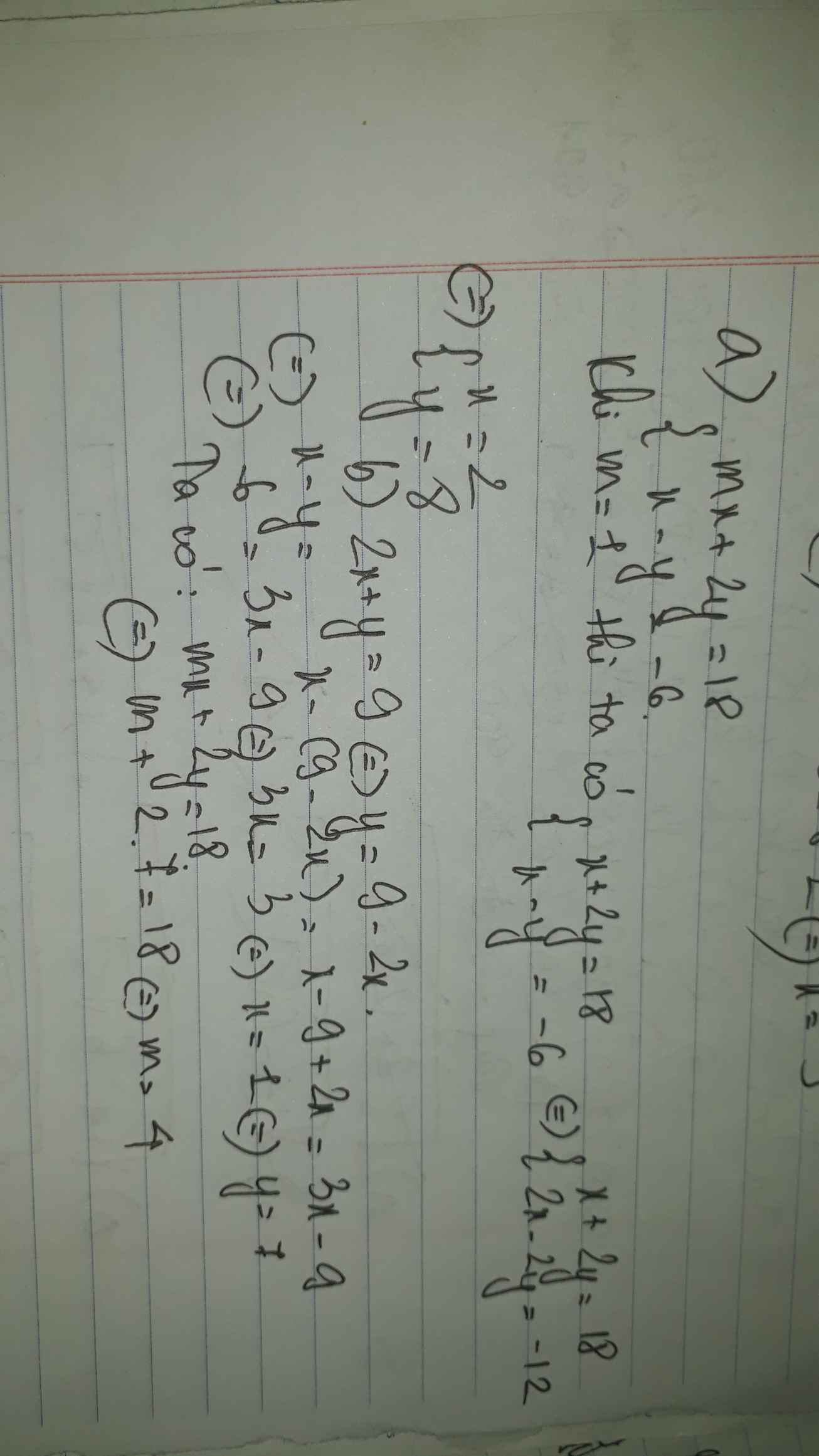
a: Khi m=-3 thì hệ phương trình sẽ là:
\(\left\{{}\begin{matrix}-3x+2y=1\\x-2\cdot\left(-3\right)\cdot y=-3-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-3x+2y=1\\x+6y=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3x+2y=1\\3x+18y=-15\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}20y=-14\\x+6y=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{7}{10}\\x=-5-6y=-5-6\cdot\dfrac{-7}{10}=\dfrac{42}{10}-5=-\dfrac{8}{10}=-\dfrac{4}{5}\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}mx+2y=1\\x-2my=m-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2my+m-2\\m\left(2my+m-2\right)+2y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2my+m-2\\2m^2\cdot y+m^2-2m+2y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2my+m-2\\y\left(2m^2+2\right)=-m^2+2m+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{-m^2+2m+1}{2m^2+2}\\x=2m\cdot\dfrac{-m^2+2m+1}{2m^2+2}+m-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{-m^2+2m+1}{2m^2+2}\\x=\dfrac{m\left(-m^2+2m+1\right)}{m^2+1}+m-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{-m^2+2m+1}{2m^2+2}\\x=\dfrac{-m^3+2m^2+m+\left(m-2\right)\left(m^2+1\right)}{m^2+1}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{-m^3+2m^2+m+m^3+m-2m^2-2}{m^2+1}=\dfrac{2m-2}{m^2+1}\\y=\dfrac{-m^2+2m+1}{2m^2+2}\end{matrix}\right.\)
x-2y=-1
=>\(\dfrac{2m-2}{m^2+1}-\dfrac{2\cdot\left(-m^2+2m+1\right)}{2m^2+2}=1\)
=>\(\dfrac{2m-2}{m^2+1}-\dfrac{-m^2+2m+1}{m^2+1}=1\)
=>\(\dfrac{2m-2+m^2-2m-1}{m^2+1}=1\)
=>\(m^2-3=m^2+1\)
=>-3=1(vô lý)