Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thay \(x=0;y=0\) vào giả thiết ta được \(f\left(0\right)=0\)
Thay \(y=0\) ta được \(f\left(x\right)+f\left(-x\right)=0\Rightarrow f\) là hàm lẻ
(Phân tích 1 chút: khi đã có hàm lẻ, ta cần thế tiếp 1 cặp sao cho "khử" được biểu thức phức tạp dạng hàm lồng đầu tiên, bằng cách tìm 1 giá trị y sao cho: \(x.f\left(y\right)-y=-\left(x+y\right)\) hoặc là \(x.f\left(y\right)-y=-\left(xy-x\right)\). Cái thứ nhất cho ta \(x.\left[f\left(y\right)+1\right]=0\Rightarrow f\left(y\right)=-1\) , nghĩa là ta chỉ cần tìm 1 hằng số c sao cho \(f\left(c\right)=-1\). Cái thứ 2 ko cho điều gì tốt nên bỏ qua. Bây giờ ta đi tìm c. Vế phải cần bằng -1, nghĩa là \(xy=-\dfrac{1}{2}\), vế trái cần khử bớt 2 số hạng. Nhưng trước khi có c thì \(f\left(x.f\left(y\right)-y\right)\) chưa khử được, nên ta cần khử cặp sau, bằng cách cho \(xy-x=-\left(x+y\right)\Rightarrow xy=-y\Rightarrow x=-1\), thay vào \(xy=-\dfrac{1}{2}\Rightarrow y=\dfrac{1}{2}\). Xong.)
Thế \(x=-1;y=\dfrac{1}{2}\) ta được:
\(f\left(-f\left(\dfrac{1}{2}\right)-\dfrac{1}{2}\right)+f\left(-\dfrac{1}{2}+1\right)+f\left(-1+\dfrac{1}{2}\right)=-1\)
\(\Leftrightarrow f\left(-f\left(\dfrac{1}{2}\right)-\dfrac{1}{2}\right)=-1\)
Đặt \(c=-f\left(\dfrac{1}{2}\right)-\dfrac{1}{2}\) là 1 hằng số nào đó
\(\Rightarrow f\left(c\right)=-1\)
Thế \(y=c\) vào ta được:
\(f\left(x.f\left(c\right)-c\right)+f\left(cx-x\right)+f\left(x+c\right)=2c.x\)
\(\Leftrightarrow f\left(-x-c\right)+f\left(x+c\right)+f\left(cx-x\right)=2c.x\)
\(\Leftrightarrow f\left(cx-x\right)=2c.x\) (1)
- Nếu \(c=1\Rightarrow f\left(0\right)=2x\) ko thỏa mãn \(f\left(0\right)=0\)
\(\Rightarrow c\ne1\), khi đó đặt \(cx-x=t\) \(\Rightarrow x=\dfrac{t}{c-1}\)
(1) trở thành \(f\left(t\right)=\dfrac{2c}{c-1}.t\)
Đặt \(\dfrac{2c}{c-1}=a\) \(\Rightarrow f\left(t\right)=a.t\)
Hay hàm cần tìm có dạng \(f\left(x\right)=ax\) với a là hằng số

a/ \(\lim\limits_{x\rightarrow\sqrt{2}}f\left(x\right)=\lim\limits_{x\rightarrow\sqrt{2}}\frac{\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)}{x-\sqrt{2}}=\lim\limits_{x\rightarrow\sqrt{2}}\left(x+\sqrt{2}\right)=2\sqrt{2}\)
\(\Rightarrow\lim\limits_{x\rightarrow\sqrt{2}}f\left(x\right)=f\left(\sqrt{2}\right)\Rightarrow\) hàm số liên tục tại \(x=\sqrt{2}\)
b/ \(\lim\limits_{x\rightarrow5^+}f\left(x\right)=\lim\limits_{x\rightarrow5^+}\frac{x-5}{\sqrt{2x-1}-3}=\frac{\left(x-5\right)\left(\sqrt{2x-1}+3\right)}{2\left(x-5\right)}=\lim\limits_{x\rightarrow5^+}\frac{\sqrt{2x-1}+3}{2}=3\)
\(f\left(5\right)=\lim\limits_{x\rightarrow5^-}f\left(x\right)=\lim\limits_{x\rightarrow5^-}\left[\left(x-5\right)^2+3\right]=5\)
\(\Rightarrow\lim\limits_{x\rightarrow5^+}f\left(x\right)=\lim\limits_{x\rightarrow5^-}f\left(x\right)=f\left(5\right)\Rightarrow\) hàm số liên tục tại \(x=5\)

d/
\(f'\left(x\right)=4cos^2\frac{x}{2}-2x.2cos\frac{x}{2}.sin\frac{x}{2}=2\left(1+cosx\right)-2x.sinx\)
\(f'\left(x\right)=g\left(x\right)\)
\(\Leftrightarrow2+2cosx-2x.sinx=8cos\frac{x}{2}-3-2sinx\)
Chà, có vẻ bạn ghi ko đúng đề, pt này ko giải được.
Chắc \(g\left(x\right)=8cos\frac{x}{2}-3-2x.sinx\) mới đúng chứ nhỉ?
c/
\(f'\left(x\right)=4x.cos^2\frac{x}{2}-2x^2.cos\frac{x}{2}.sin\frac{x}{2}=2x\left(1+cosx\right)-x^2sinx\)
\(f'\left(x\right)=g\left(x\right)\)
\(\Leftrightarrow2x\left(1+cosx\right)-x^2sinx=x-x^2sinx\)
\(\Leftrightarrow2x\left(1+cosx\right)=x\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\2\left(1+cosx\right)=1\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow cosx=-\frac{1}{2}\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{2\pi}{3}+k2\pi\\x=-\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)

Lời giải:
Cái này chỉ tính được giới hạn 1 bên thôi
\(\lim\limits_{x\to 1-}f(x)=\lim\limits_{x\to 1-}\frac{x^2+1}{1-x}=+\infty \) do $\lim\limits_{x\to 1-}(x^2+1)=2>0$ và $1-x>0$ với $x<1$
\(\lim\limits_{x\to 1+}\sqrt{2x-2}=\sqrt{2.1-2}=0\)

a: \(\lim\limits_{x\rightarrow3^+}f\left(x\right)=\lim\limits_{x\rightarrow3^+}x^2-3=3^2-3=6\)
\(\lim\limits_{x\rightarrow3^-}f\left(x\right)=\lim\limits_{x\rightarrow3^-}x+3=3+3=6\)
b: Vì \(\lim\limits_{x\rightarrow3^+}f\left(x\right)=\lim\limits_{x\rightarrow3^-}f\left(x\right)=6\)
nên hàm số tồn tại lim khi x=3
=>\(\lim\limits_{x\rightarrow3}f\left(x\right)=6\)

a.
\(\lim\limits_{x\rightarrow+\infty}\left(\sqrt[3]{x^3+4x^2}-x\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{4x^2}{\sqrt[3]{\left(x^3+4x^2\right)^2}+x\sqrt[3]{x^3+4x^2}+x^2}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{4}{\sqrt[3]{\left(1+\dfrac{4}{x}\right)^2}+\sqrt[3]{1+\dfrac{4}{x}}+1}=\dfrac{4}{1+1+1}=\dfrac{4}{3}\)
b.
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\dfrac{4x-1}{x-1}=\dfrac{3}{0}=+\infty\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\left(7x+1\right)=8\)

• Xét hàm số \(f\left( x \right) = 2x - \sin x\) có tập xác định \(D = \mathbb{R}\).
Vậy hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\).
• Xét hàm số \(g\left( x \right) = \sqrt {x - 1} \)
ĐKXĐ: \(x - 1 \ge 0 \Leftrightarrow x \ge 1\)
Hàm số \(g\left( x \right) = \sqrt {x - 1} \) có tập xác định \(D = \left[ {1; + \infty } \right)\).
Hàm số \(g\left( x \right) = \sqrt {x - 1} \) là hàm căn thức nên liên tục trên khoảng \(\left( {1; + \infty } \right)\).
Ta có: \(\mathop {\lim }\limits_{x \to {1^ + }} g\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \sqrt {x - 1} = \sqrt {1 - 1} = 0 = g\left( 1 \right)\)
Do đó hàm số \(g\left( x \right) = \sqrt {x - 1} \) liên tục tại điểm \({x_0} = 1\).
Vậy hàm số \(g\left( x \right) = \sqrt {x - 1} \) liên tục trên nửa khoảng \(\left[ {1; + \infty } \right)\).
• Xét hàm số \(y = f\left( x \right).g\left( x \right) = \left( {2x - \sin x} \right)\sqrt {x - 1} \)
Do hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) đều liên tục tại mọi điểm \({x_0} \in \left[ {1; + \infty } \right)\) nên hàm số \(y = f\left( x \right).g\left( x \right)\) liên tục trên nửa khoảng \(\left[ {1; + \infty } \right)\).
• Xét hàm số \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{2x - \sin x}}{{\sqrt {x - 1} }}\)
Do hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) đều liên tục tại mọi điểm \({x_0} \in \left[ {1; + \infty } \right)\) nên hàm số \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục trên khoảng \(\left( {1; + \infty } \right)\).


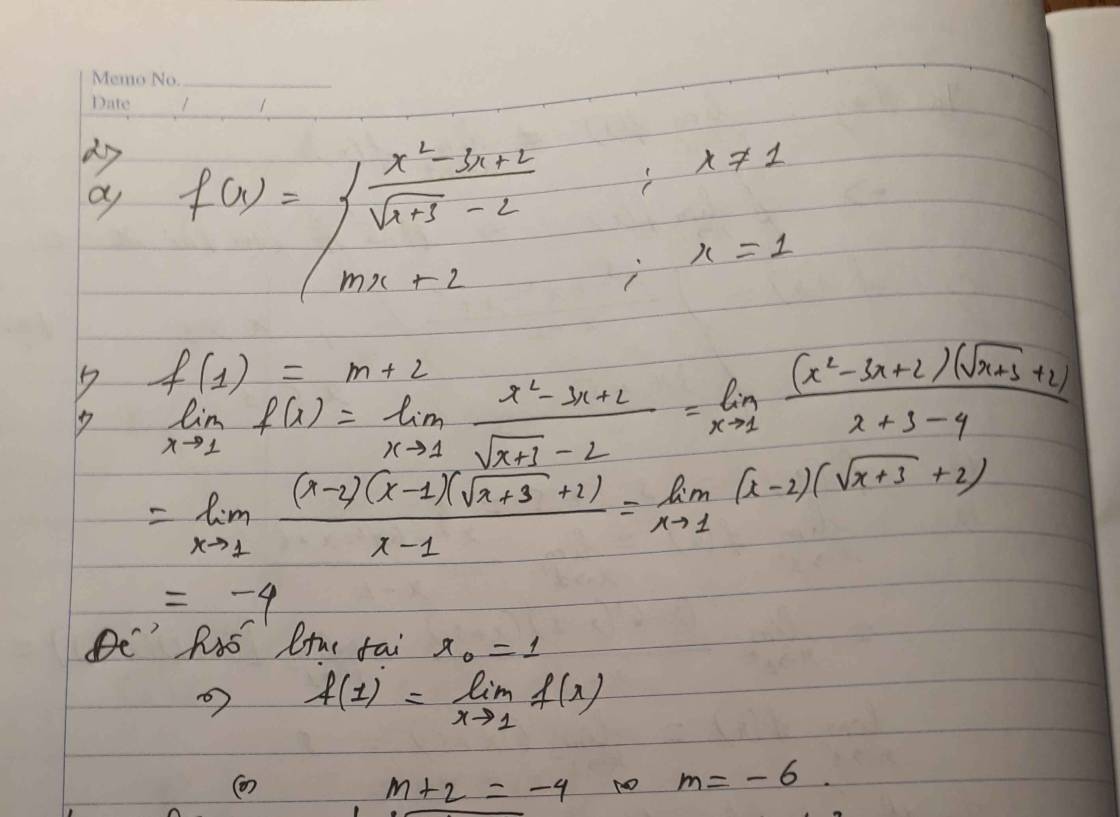
Thay \(y=0\Rightarrow f\left(x\right)=f\left(x\right)+f\left(0\right)\Rightarrow f\left(0\right)=0\)
Đặt \(g\left(x\right)=f\left(x\right)-x^2\Rightarrow g\left(0\right)=0\)
\(g\left(x+y\right)=f\left(x+y\right)-\left(x+y\right)^2=f\left(x\right)+f\left(y\right)+2xy-\left(x+y\right)^2\)
\(=\left[f\left(x\right)-x^2\right]+\left[f\left(y\right)-y^2\right]=g\left(x\right)+g\left(y\right)\)
Vậy quy về tìm hàm \(g\) thỏa \(g\left(x+y\right)=g\left(x\right)+g\left(y\right)\)
\(g\left(x+\Delta x\right)=g\left(x\right)+g\left(\Delta x\right)\Rightarrow g\left(x+\Delta x\right)-g\left(x\right)=g\left(\Delta x\right)-g\left(0\right)\)
\(\Rightarrow\frac{g\left(x+\Delta x\right)-g\left(x\right)}{\Delta x}=\frac{g\left(\Delta x\right)-g\left(0\right)}{\Delta x}\)
Lấy giới hạn 2 vế: \(\lim\limits_{\Delta x\rightarrow0}\frac{g\left(x+\Delta x\right)-g\left(x\right)}{\Delta x}=\lim\limits_{\Delta x\rightarrow0}\frac{g\left(\Delta x\right)-g\left(0\right)}{\Delta x}\)
\(\Leftrightarrow g'\left(x\right)=g'\left(0\right)=const\) (theo định nghĩa về đạo hàm)
\(\Rightarrow g\left(x\right)=c.x\) với c là hằng số
\(\Rightarrow f\left(x\right)=x^2+cx\)
Thay vào pt dưới: \(\left(\frac{1}{x}\right)^2+c\left(\frac{1}{x}\right)=\frac{x^2+cx}{x^4}=\left(\frac{1}{x}\right)^2+c\left(\frac{1}{x^3}\right)\)
\(\Leftrightarrow c\left(\frac{1}{x}\right)=c\left(\frac{1}{x^3}\right)\)
Điều này thỏa mãn với mọi x khi và chỉ khi \(c=0\)
\(\Rightarrow f\left(x\right)=x^2\Rightarrow f\left(\sqrt{2019}\right)=2019\)
Nguyễn Việt Lâm a thi VMO k thế :D