Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
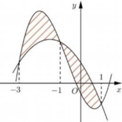
Ta có đạo hàm : f’ (x) = 3ax2+ 2bx+ c.
Dựa vào đồ thị hàm số y= f’ ( x) ta thấy đồ thị hàm số y= f’ (x) đi qua 3 điểm
( -1; 0) ; (3; 0) ; (1; -4)
Thay tọa độ 3 điểm này vào hàm f’ ta tìm được: a= 1/3; b= -1; c= -3.
Suy ra: f’ (x) = x2-2x-3 và f(x) = 1/3.x3-x2-3x+d.
Do (C) tiếp xúc với đường thẳng y= -9 tại điểm có hoành độ dương nên ta có:
F’(x) =0 khi và chỉ khi x=3 ( x= -1 bị loại vì âm)
Như vậy (C) đi qua điểm (3; -9) ta tìm được d=0.
Vậy hàm số đề bài cho là f(x) = 1/3.x3-x2-3x.
Xét phương trình trình hoành độ giao điểm và trục hoành:
. 1 3 x 3 - x 2 - 3 x = 0 ⇔ x = 0 ; x = 3 ± 3 5 2 S = ∫ 3 - 3 5 2 3 + 3 5 2 1 3 x 3 - x 2 - 3 x d x = 29 , 25
Chọn C.
+Ta có đạo hàm f’ (x)= 3ax2+ 2bx+c .
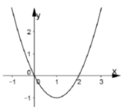
+ Dựa vào đồ thị hàm số y= f’ ( x) ta thấy đồ thị hàm số đi qua các điểm (0 ; 0) ; (1 ; -1) ; (2 ; 0) nên a= 1/3 ; b= -1 ; c= 0.
Do vậy hàm số cần tìm có dạng y= 1/3 x3-x2+ d .
Điểm tiếp xúc với trục hoành là cực trị của đồ thị hàm số và tại đó ta có x= 0 hoặc x= 2. + Vì đồ thị hàm số y= f(x) tiếp xúc với trục hoành tại điểm có hoành độ dương nên đồ thị hàm số tiếp xúc trục hoành tại điểm x= 2 nghĩa là:
f( 2) = 0 hay 8/3-4+ d= 0 nên d= 4/3
Chọn D.
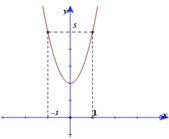
Ta có đạo hàm : f’ (x) = 3ax2+ 2bx+ c.
Dựa vào đồ thị hàm số y= f’(x) ; ta thấy đồ thị hàm số y= f’(x) là parabol có trục đối xứng là trục tung nên b= 0
+ Đồ thị hàm số y= f’(x) đi qua 2 điểm (1; 5) và (0; 2) ta tìm được: a=1 và c=2.
Suy ra: f’(x) = 3x2+ 2 và f( x) = x3+ 2x+ d,
+ Do đồ thị hàm số (C) đi qua gốc toạ độ nên 0=0+0+ d
Suy ra: d= 0.
Khi đó ta có: f(x) =x3+ 2x và f( 3) –f(2) =21
Chọn D.
.
.
.
.
+ Từ đồ thị của hàm số và a> 0 ta dễ dàng có được đồ thị hàm số y= f’(x) như sau:
Ta có : f’(x) = 4ax3+ 2bx
Đồ thị hàm số y= f’(x) đi qua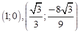 
ta tìm được a=1 và b= -2
Suy ra hàm số đã cho có dạng: f(x) =x4-2x2+d và f’(x) = 4x3-4x.
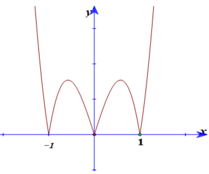
+ Do (C) tiếp xúc với trục hoành nên f’(x) = 0 khi x=0; x=1; x=- 1.
Do (C) đối xứng qua trục tung nên (C) tiếp xúc với trục hoành tại 2 điểm (1; 0) và (-1; 0).
Do đó: f(0) =1 suy ra 1= 0-2.0+ d nên d= 1
Vậy hàm số cần tìm là: y =x4-2x2+1
+ Xét phương trình hoành độ giao điểm của (C) với trục hoành:
x4-2x2+1 =0 nên x=± 1
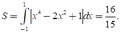
Chọn D.
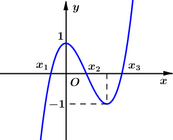
Có thể nghịch suy để chọn hàm làm trắc nghiệm
Do \(x_2=\dfrac{x_3-x_1}{2}=1\) nên hàm có dạng: \(y=a\left(x-1\right)^4-b\left(x-1\right)^2+c\) với a;b;c dương
\(y'=0\Rightarrow\left[{}\begin{matrix}x-1=0\\\left(x-1\right)^2=\dfrac{b}{2a}\end{matrix}\right.\) \(\Rightarrow x_1;x_3\) thỏa mãn \(\left(x-1\right)^2=\dfrac{b}{2a}\) và \(f\left(x_2\right)=c\)
\(f\left(x_1\right)+f\left(x_3\right)+\dfrac{2}{3}f\left(x_2\right)=0\Leftrightarrow2f\left(x_1\right)+\dfrac{2}{3}f\left(x_2\right)=0\)
\(\Leftrightarrow a.\left(\dfrac{b}{2a}\right)^2-b\left(\dfrac{b}{2a}\right)+c+\dfrac{c}{3}=0\Rightarrow-\dfrac{b^2}{4a}+\dfrac{4c}{3}=0\)
Tới đây chọn \(a=3;c=1;b=4\) được hàm \(f\left(x\right)=3\left(x-1\right)^4-4\left(x-1\right)^2+1\)
Dễ dàng tính ra \(x_3=1+\sqrt{\dfrac{2}{3}}\) ; \(x_0=1+\sqrt{\dfrac{1}{3}}\) (với \(x_0\) là giao bên phải của đồ thị và trục hoành); \(f\left(x_1\right)=f\left(x_3\right)=-\dfrac{1}{3}\)
\(S_1+S_2=\int\limits^{x_0}_1f\left(x\right)dx-\int\limits^{x_3}_{x_0}f\left(x\right)dx\approx0,41\)
\(\dfrac{S_1+S_2}{S_3+S_4}=\dfrac{0,41}{\left(1+\dfrac{1}{3}\right)\left(x_3-1\right)-0,41}\approx0,6\)
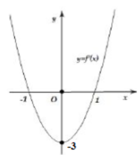
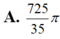
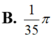
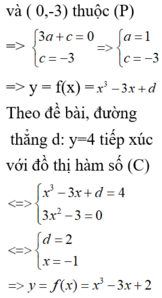
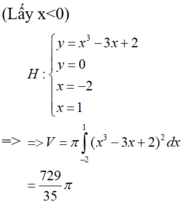
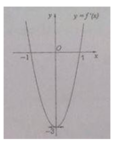
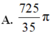
+ Ta có đạo hàm : f’ (x) = 3ax2+ 2bx+ c.
Dựa vào đồ thị hàm số y= f’( x), ta thấy đồ thị hàm số y= f’ (x) là parabol có trục đối xứng là trục tung nên b=0
Đồ thị hàm số y= f’( x) đi qua 2 điểm (1;0) và (0; -3) thay vào f’(x) ; ta tìm được: a=1 và c= -3.
Suy ra: f’(x) = 3x2-3b và f(x) = x3-3x+d.
+ Do (C) tiếp xúc với đường thẳng y= 4 tại điểm có hoành độ âm nên ta có:
f’(x) =0 khi và chỉ khi x= -1;x= 1( loại)
Như vậy (C) đi qua điểm (-1; 4) ta tìm được d= 2
Khi đó; f( x) =x3-3x+2.
chọn A.