Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(M\left(x_0;\frac{2x_0-1}{x_0-1}\right);x_0\ne-1\) là tiếp điểm.
Theo đề bài ta có MA = 2
hay \(x^2_0+\left(\frac{2x_0-1}{x_0+1}-1\right)^2=4\Leftrightarrow x^2_0+\left(\frac{x_0-2}{x_0+1}\right)^2=4\)
\(\Leftrightarrow x_0\left(x_0-2\right)\left(x^2_0+4x_0+6\right)=0;\left(x_0\ne-1\right)\Leftrightarrow\left[\begin{array}{nghiempt}x_0=0\\x_0=2\end{array}\right.\)
* Với \(x_0=0\), phương trình tiếp tuyến là \(y=y'\left(0\right)\left(x-0\right)+y\left(0\right)\) hay \(y=3x-1\)
* Với \(x_0=2\), phương trình tiếp tuyến là \(y=y'\left(2\right)\left(x-2\right)+y\left(2\right)\) hay \(y=\frac{1}{3}x+\frac{1}{3}\)
Vậy có tiếp tuyến thỏa mãn bài toán \(y=\frac{1}{3}x+\frac{1}{3}\) và \(y=3x-1\)

+ Đồ thi hàm số đã cho co TCĐ là : x= -1 và TCN là y= 1; tâm đối xứng- giao của 2 đườg tiệm cận có tọa độ là I ( -1; 1)
Gọi M x 0 ; x 0 - 2 x 0 + 1 ∈ C , x 0 ≠ - 1 , I ( - 1 ; 1 )
+ Phương trình tiếp tuyến tại M có dạng
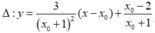
+ Giao điểm của ∆ với tiệm cận đứng là A - 1 ; x 0 - 5 x 0 + 1
+ Giao điểm của ∆ với tiệm cận ngang là B( 2x0+1; 1).
Ta có 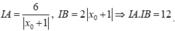
Bán kính đường tròn ngoại tiếp tam giác IAB là S=p.r, suy ra
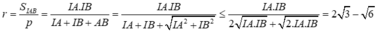
Suy ra,
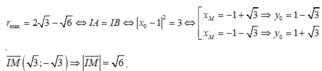
Chọn D.

Gọi \(x_0\) là hoành độ tiếp điểm \(\left(x_0\ne-1\right)\), phương trình tiếp tuyến là :
\(y=\frac{1}{\left(x_0+1\right)^2}\left(x-x_0\right)+\frac{2x_0+1}{x_0+1}\)
Vì tiếp tuyến cách đều A và b nên tiếp tuyến đi qua trung điểm I của AB hoặc song song AB.
- Nếu tiếp tuyến đi qua trung điểm I(-1;1) của AB ta có \(x_0=1\), vậy phương trình là \(y=\frac{1}{4}x+\frac{5}{4}\)
- Nếu tiếp tuyến song song với đường thẳng AB : \(y=x+2\), ta có :
\(\frac{1}{\left(x_0+1\right)^2}=1;\frac{2x_0+1}{x_0+1}\ne2\Rightarrow x_0=0;x_0=-2\)
Với \(x_0=0\) ta có : \(y=x+1\)
Với \(x_0=-2\) ta có : \(y=x+5\)

a. Ta có : \(y'=3x^2-6x+2\)
\(x_0=1\Leftrightarrow y_0=-6\) và \(y'\left(x_0\right)=y'\left(-1\right)=11\)
Suy ra phương trình tiếp tuyến là \(y=y'\left(-1\right)\left(x+1\right)-6=11x+5\)
b. Gọi \(M\left(x_0;6\right)\) là tiếp điểm, ta có :
\(x_0^3-3x_0^2+2x_0=6\Leftrightarrow\left(x_0-3\right)\left(x_0^2+2\right)=0\Leftrightarrow x_0=3\)
Vậy phương trình tiếp tuyến là :
\(y=y'\left(3\right)\left(x-3\right)+6=11x-27\)
c. PTHD giao điểm của (C) với Ox :
\(x^3-3x^2+2x=0\Leftrightarrow x=0;x=1;x=2\)
* \(x=0\) ta có tiếp tuyến : \(y=y'\left(0\right)\left(x-0\right)+0=2x\)
* \(x=1\) ta có tiếp tuyến : \(y=y'\left(1\right)\left(x-1\right)+0=-x+1\)
* \(x=2\) ta có tiếp tuyến : \(y=y'\left(2\right)\left(x-2\right)+0=2x-4\)

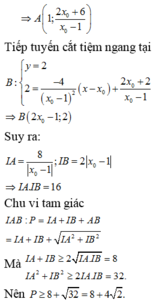
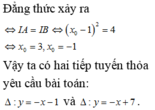


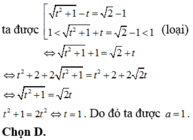

\(y'=\dfrac{3}{\left(x+1\right)^2}\)
Gọi \(M\left(m;\dfrac{2m-1}{m+1}\right)\) là tiếp điểm
Phương trình tiếp tuyến tại M:
\(y=\dfrac{3}{\left(m+1\right)^2}\left(x-m\right)+\dfrac{2m-1}{m+1}\)
\(\Leftrightarrow3x-\left(m+1\right)^2y+2m^2-2m-1=0\)
Áp dụng công thức khoảng cách:
\(\dfrac{\left|-\left(m+1\right)^2+2m^2-2m-1\right|}{\sqrt{9+\left(m+1\right)^4}}=1\)
Bạn tự giải ra m nhé