Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B. Thay \(\dfrac{1}{3}\)vào x và \(\dfrac{1}{2}\)vào y
giải để ra được m

\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
\(\left\{{}\begin{matrix}\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a-b}{c-d}\\\dfrac{a}{c}=\dfrac{b}{d}\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}\left(\dfrac{a}{c}\right)^2=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\\\left(\dfrac{a}{c}\right)^2=\dfrac{ab}{cd}\end{matrix}\right.\)
\(\Rightarrow\dfrac{ab}{cd}=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\)

Thay hoành độ điểm A vào công thức hàm số, ta có:
y=5.(12)2−2=54−2=54−84=−34=yAy=5.(12)2−2=54−2=54−84=−34=yA
Vậy A(12;−34)A(12;−34) thuộc đồ thị hàm số.
Thay hoành độ điểm B vào công thức hàm số, ta có:
y=5.(12)2−2=54−2=54−84=−34≠yBy=5.(12)2−2=54−2=54−84=−34≠yB
Vậy điểm B không thuộc đồ thị hàm số
Thay hoành độ điểm C vào công thức hàm số, ta có:
y=5.22−2=5.4−2=20−2=18=yCy=5.22−2=5.4−2=20−2=18=yC
Vậy C(2;18) thuộc đồ thị hàm số.

câu a gồm : A(6: -2) , E( 0; 0)
câu b gồm : B( -2; -10 ) ,E ( 0: 0)

+)Thay xA=\(\dfrac{-1}{3}\) vào hàm số y=3x-1:
y=\(3.\dfrac{-1}{3}-1=-1-1=-2\ne y_A\)
A ko thuộc đồ thị hàm số y=3x-1.
+)Thay xB=\(\dfrac{1}{3}\)vào hàm số y=3x-1:
y=\(\dfrac{1}{3}.3-1=1-1=0=y_B\)
B thuộc đồ thi hàm số y=3x-1.
+)Thay xC=0 vào hàm số y=3x-1:
y=\(0.\dfrac{1}{3}-1=0-1=-1\ne y_C\)
C ko thuộc đồ thị hàm số y=3x-1.
+)Thay xD=0 vào hàm số y=3x-1:
y=\(0.\dfrac{1}{3}-1=0-1=-1=y_D\)
D thuộc đồ thị hàm số y=3x-1.
Vậy điểm B,D ko thuộc đồ thị hàm số y=3x-1.
Ta có: 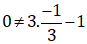
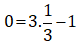
1 ≠ 3.0 – 1 nên điểm C không thuộc đồ thị hàm số y = 3x – 1.
-1 = 3.0 – 1 nên điểm D thuộc đồ thị hàm số y = 3x – 1.

Bài 1:
Áp dụng t.c của dãy tỉ số bằng nhau, ta có:
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{a+b+c}{b+c+d}\\ =\left(\dfrac{a+b+c}{b+c+d}\right)^3=\dfrac{a^3}{b^3}=\dfrac{a.b.c}{b.c.d}=\dfrac{a}{d}\left(dpcm\right)\)

Bài 1:
Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk; c=dk\)
Khi đó: \(\left\{\begin{matrix} \frac{2a+5b}{3a-4b}=\frac{2bk+5b}{3bk-4b}=\frac{b(2k+5)}{b(3k-4)}=\frac{2k+5}{3k-4}\\ \frac{2c+5d}{3c-4d}=\frac{2dk+5d}{3dk-4d}=\frac{d(2k+5)}{d(3k-4)}=\frac{2k+5}{3k-4}\end{matrix}\right.\)
\(\Rightarrow \frac{2a+5b}{3a-4b}=\frac{2c+5d}{3c-4d}\)
Ta có đpcm.
Bài 2:
Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk; c=dk\)
Khi đó: \(\frac{ab}{cd}=\frac{bk.b}{dk.d}=\frac{b^2}{d^2}\)
\(\frac{a^2+b^2}{c^2+d^2}=\frac{(bk)^2+b^2}{(dk)^2+d^2}=\frac{b^2(k^2+1)}{d^2(k^2+1)}=\frac{b^2}{d^2}\)
Do đó: \(\frac{ab}{cd}=\frac{a^2+b^2}{c^2+d^2}(=\frac{b^2}{d^2})\) . Ta có đpcm.

Theo tính chất dãy tỉ số bằng nhau, ta có:
a/b = b/c = c/d = (a + b + c)/(b + c + d)
--> ((a + b + c)/(b + c + d))^3 = a^3/b^3
Cần chứng minh:
a^3/b^3 = a/d
<=> a^3/b^3 = a^3/(a^2.d)
--> b^3 = a^2.d
Mà ad = bc (do a/b = c/d)
--> b^3 = abc
<=> b^2 = ac (luôn đúng do a/b = b/c)
--> đpcm