Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D.
Phương trình đường thẳng d có hệ số góc k và đi qua I(1; 2) là d: y = k(x - 1) + 2.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d:
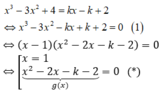
Để d cắt (C) tại ba điểm phân biệt ⇔ Phương trình (*) có hai nghiệm phân biệt x1; x2 khác 1.
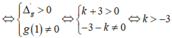
Hơn nữa theo Viet ta có
nên I là trung điểm AB.
Vậy chọn k > -3, hay k ∈ (-3;+∞).
Phương trình đường thẳng d; y=k(x-1)+2.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d:
x3-3x2+4= k(x-1)+2. Hay x3-3x2-kx+k+2= 0 (1)
⇔
(
x
-
1
)
(
x
2
-
2
x
-
k
-
2
)
=
0
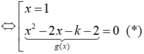
( C) cắt d tại ba điểm phân biệt khi và chỉ khi phương trình có hai nghiệm phân biệt x1; x2 khác 1
⇔ ∆ ' g > 0 g ( 1 ) ≠ 0 ⇔ k + 3 > 0 - 3 - k ≠ 0 ⇔ k > - 3
Hơn nữa theo Viet ta có
x 1 + x 2 = 2 = 2 x I y 1 + y 2 = k ( x 1 + x 2 ) - 2 k + 4 = 4 = 2 y I
nên I là trung điểm AB.
Vậy chọn k> -3, hay k ∈ (-3; +∞). Do đó có vô số giá trị k nguyên thỏa mãn yêu cầu bài toán.
Chọn D.
Đường thẳng d đi qua A và có hệ số góc k nên có dạng y= k( x+ 1) hay
Kx- y+k=0 .
Phương trình hoành độ giao điểm của C và d là:
x 3 - 3 x 2 + 4 = k x + k ⇔ ( x + 1 ) ( x 2 - 4 x + 4 - k ) = 0
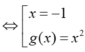
D cắt tại ba điểm phân biệt khi phương trình (*) có hai nghiệm phân biệt khác -1
⇔ ∆ ' > 0 g ( - 1 ) ≠ 0 ⇔ k > 0 k ≠ 9
Khi đó g( x) =0 khi x=2- k ; x = 2 + k Vậy các giao điểm của hai đồ thị lần lượt là
A ( - 1 ; 0 ) ; B ( 2 - k ; 3 k - k k ) ; C ( 2 + k ; 3 k + k k ) .
Tính được
B C = 2 k 1 + k 2 , d ( O , B C ) = d ( O , d ) = k 1 + k 2 .
Khi đó
S ∆ O B C = 1 2 . k k 2 + 1 . 2 k . k 2 + 1 = 1 ⇔ k k = 1 ⇔ k 3 = 1 ⇔ k = 1 .
Vậy k= 1 thỏa yêu cầu bài toán.
Chọn C.
+ Phương trình đường thẳng d có dang d: y= kx-1 .
Phương trình hoành độ giao điểm của đồ thị C và đường thẳng d:
2
x
3
-
3
x
2
-
1
=
k
x
-
1
h
a
y
x
(
2
x
2
-
3
x
-
k
)
=
0
⇔
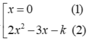
+ Để C cắt d tại ba điểm phân biệt khi và chỉ khi phương trình (2) có hai nghiệm phân biệt khác 0
⇔ ∆ > 0 0 - k ≠ 0 ⇔ k > - 9 8 k ≠ 0
Vậy chọn k > - 9 8 k ≠ 0
Chọn B.
+ Hoành độ giao điểm là nghiệm của phương trình
x3- 3x2-m+ 2= -mx hay ( x-1) ( x2-2x+ m-2) =0
Hay x=1; x2-2x+m-2=0
+ Đặt nghiệm x2= 1; từ giải thiết bài toán trở thành tìm m để phương trình có 3 nghiệm lập thành cấp số cộng. Khi đó phương trình : x2-2x+m-2 = 0 phải có 2 nghiệm phân biệt (vì theo hệ thức Viet ta có: x1+ x3= 2= 2x2 ).
Vậy khi đó ta cần ∆’ > 0( để phương trình có 2 nghiệm phân biệt )
∆’=1-(m-2)>0 ⇔ m < 3
Chọn C.
Chọn C
.
Vì 
nên phương trình 
có 2 nghiệm phân biệt.
Do đó hàm số có hai điểm cực trị 
.
Giả sử hàm số có hai điểm cực trị lần lượt là 
và 
, với 
, 
là nghiệm của phương trình 
.
Thực hiện phép chia 
cho 
ta được : 
.
Khi đó ta có: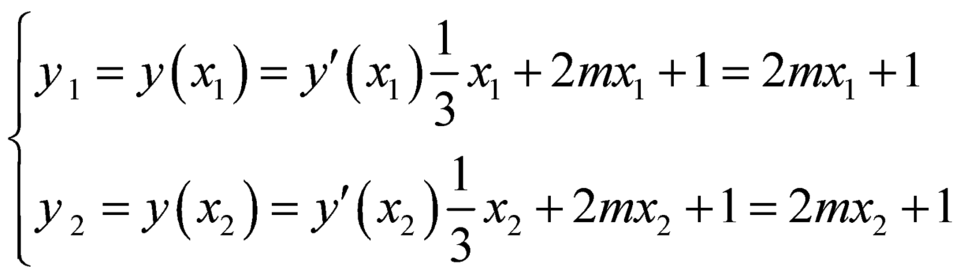 
.
Ta thấy, toạ độ hai điểm 
và 
thoả mãn phương trình 
.
Do đó, phương trình đường thẳng qua hai điểm cực trị là 
.
Ta thấy 
luôn qua 
.
Đặt 
.
.
Xét hàm số 
, 
.
, 
.
Suy ra hàm số 
liên tục và đồng biến trên 
.
Do đó 
.
Vậy 
đạt giá trị lớn nhất 
.
a) y = x 3 − (m + 4) x 2 − 4x + m
⇔ ( x 2 − 1)m + y − x 3 + 4 x 2 + 4x = 0
Đồ thị của hàm số (1) luôn luôn đi qua điểm A(x; y) với mọi m khi (x; y) là nghiệm của hệ phương trình:
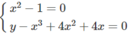
Giải hệ, ta được hai nghiệm:
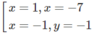
Vậy đồ thị của hàm số luôn luôn đi qua hai điểm (1; -7) và (-1; -1).
b) y′ = 3 x 2 − 2(m + 4)x – 4
Δ′ = ( m + 4 ) 2 + 12
Vì Δ’ > 0 với mọi m nên y’ = 0 luôn luôn có hai nghiệm phân biệt (và đổi dấu khi qua hai nghiệm đó). Từ đó suy ra đồ thị của (1) luôn luôn có cực trị.
c) Học sinh tự giải.
d) Với m = 0 ta có: y = x 3 – 4 x 2 – 4x.
Đường thẳng y = kx sẽ cắt (C) tại ba điểm phân biệt nếu phương trình sau có ba nghiệm phân biệt: x 3 – 4 x 2 – 4x = kx.
Hay phương trình x 2 – 4x – (4 + k) = 0 có hai nghiệm phân biệt khác 0, tức là:
