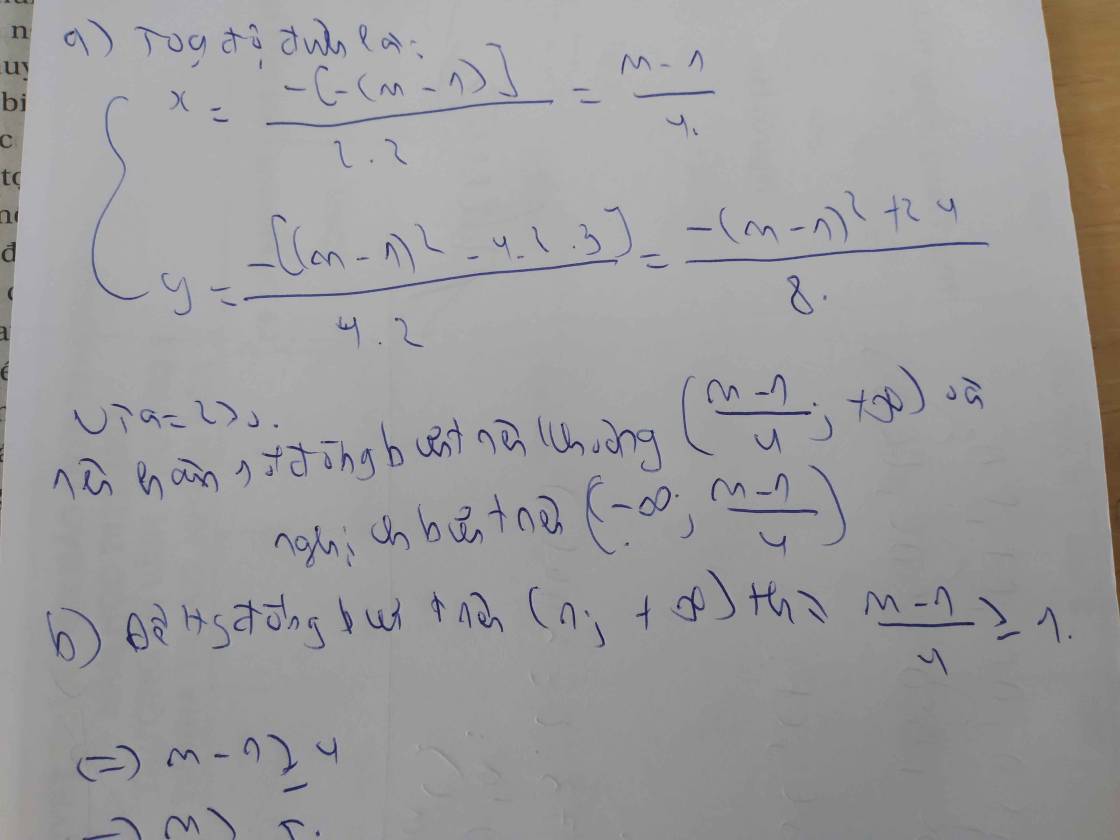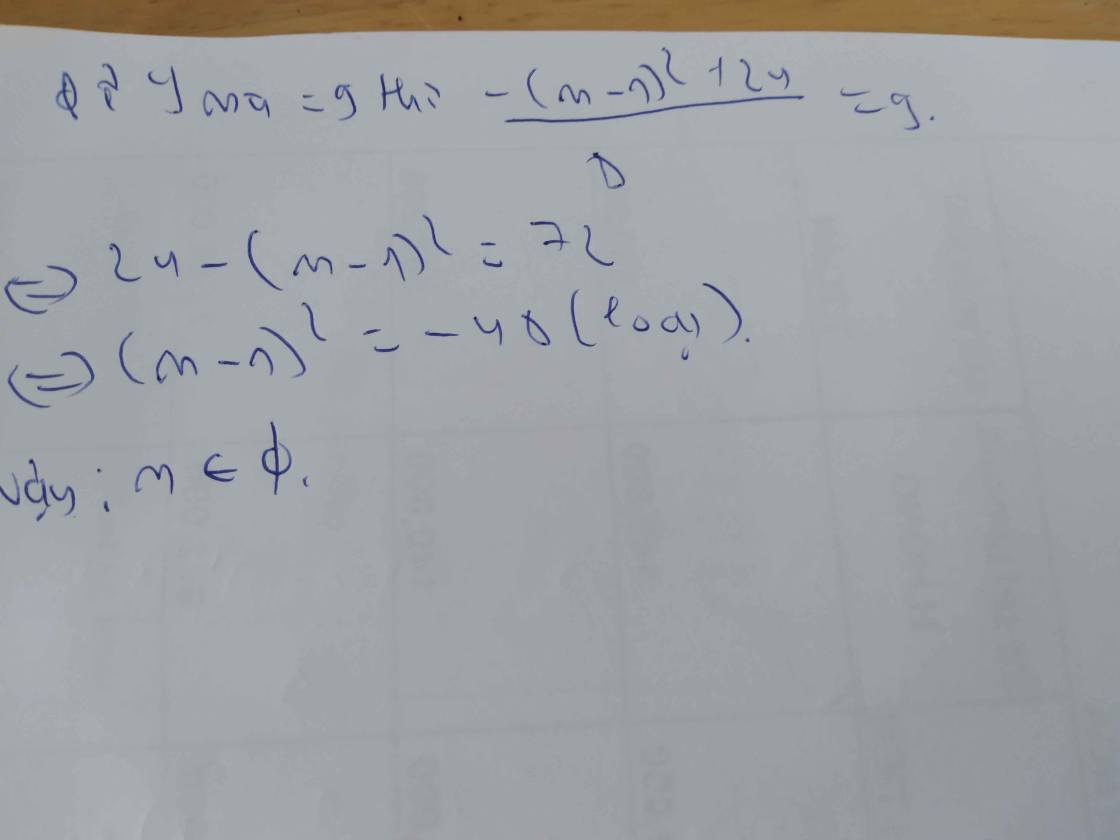Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tròi oi a viết chữ xấu wá đi à, đọc bài của a mà đau mắt wá

Hàm là \(y=mx^2-\left(m^2+1\right)x+3\) đúng không nhỉ?
- Với \(m=0\) hàm nghịch biến trên R (không thỏa)
- Với \(m\ne0\) hàm số đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}m>0\\\dfrac{m^2+1}{2m}\le1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m>0\\m^2+1\le2m\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m>0\\\left(m-1\right)^2\le0\end{matrix}\right.\)
\(\Rightarrow m=1\)

b, \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1\le x\le3\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi phương trình \(f\left(x\right)=x^2-2mx+m^2-9\ge0\) có nghiệm \(x\in\left[-1;3\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2-m^2+9=9>0,\forall m\\-1< m< 3\\f\left(-1\right)=m^2+2m-8\ge0\\f\left(3\right)=m^2-6m\ge0\end{matrix}\right.\)
\(\Leftrightarrow m\in[2;3)\cup(-1;0]\)