OLM cung cấp gói bải giảng điện tử PPT cho giáo viên đầu năm học

Thi thử và xem hướng dẫn giải chi tiết đề tham khảo 12 môn thi Tốt nghiệp THPT 2025

Tham gia cuộc thi "Nhà giáo sáng tạo" ẫm giải thưởng với tổng giá trị lên đến 10 triệu VNĐ

Mini game 20/11 tri ân thầy cô, nhận thưởng hấp dẫn - Tham gia ngay!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
B
Buddy
13 tháng 8 2023
Cho hàm số lôgarit \(y = {\log _2}x\)a)     Tìm giá trị y tương ứng với giá trị của x trong bảng sau:b,     Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a.Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;{{\log }_2}x} \right)\) với \(x \in (0; + \infty )\) và nối lại ta được đồ thị hàm số \(y = {\log _2}x\) như hình bên.c,     Cho biết tọa độ giao điểm của đồ thị hàm số \(y...
Đọc tiếp

Cho hàm số lôgarit \(y = {\log _2}x\)

a)     Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

b,     Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a.

Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;{{\log }_2}x} \right)\) với \(x \in (0; + \infty )\) và nối lại ta được đồ thị hàm số \(y = {\log _2}x\) như hình bên.

c,     Cho biết tọa độ giao điểm của đồ thị hàm số \(y = {\log _2}x\) với trục hoành và vị trí của đồ thị hàm số đó với trục tung.

d,   Quan sát đồ thị hàm số \(y = {\log _2}x\), nêu nhận xét về:

\(\mathop {\mathop {\lim }\limits_{x \to {0^ + }} ({{\log }_2}x)}\limits_{} \,;\mathop {\,\,\mathop {\lim }\limits_{x \to  + \infty } ({{\log }_2}x)}\limits_{} \)Sự biến thiên của hàm số \(y = {\log _2}x\) và lập bảng biến thiên của hàm số đó
#Toán lớp 11
1
NL
Nguyễn Lê Phước Thịnh
22 tháng 9 2023

a: 

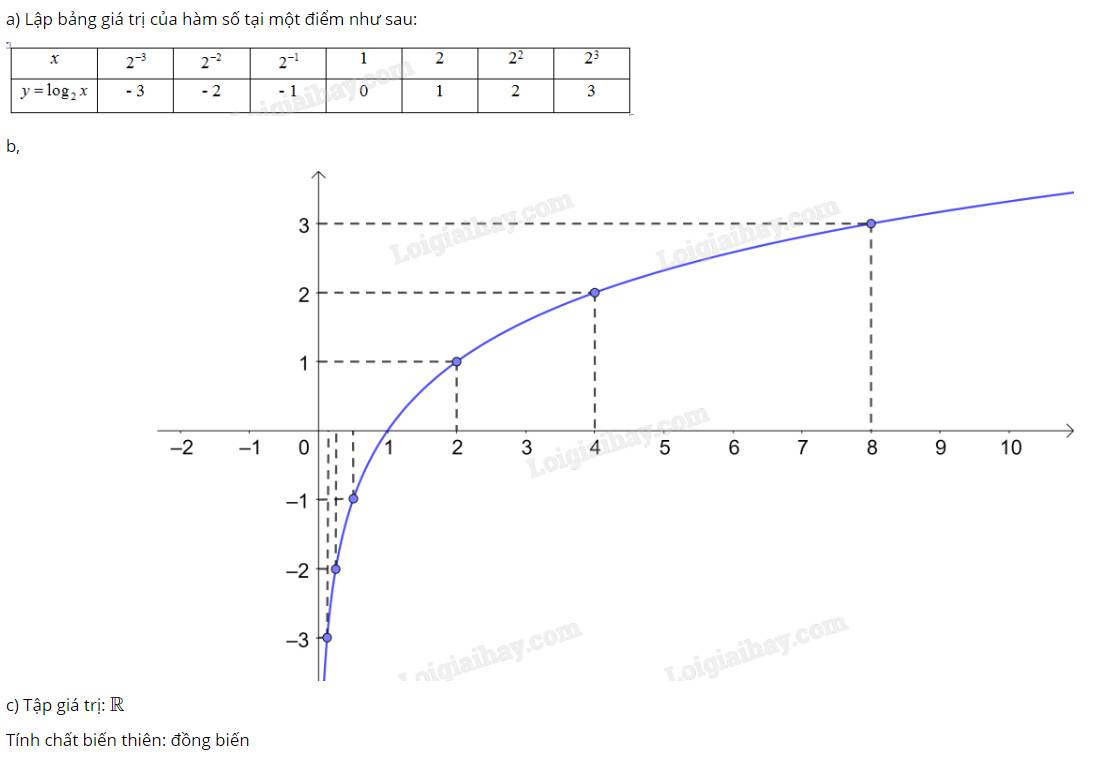
x0,51248
\(y\)-10123

b:

c: Tọa độ giao điểm của hàm số với trục hoành là B(2;0)

Đồ thị hàm số này ko cắt trục tung

d: 

\(\lim\limits_{x\rightarrow0^+}log_2x=0\)

\(\lim\limits_{x\rightarrow+\infty}\left(log_2x\right)=+\infty\)

=>Hàm số này đồng biến trên TXĐ của nó là D=[0;+vô cực)

Đúng(0)
B
Buddy
20 tháng 8 2023
a) Xét hàm số \(y = {\log _2}x\) với tập xác định \(D = \left( {0; + \infty } \right)\).i) Hoàn thành bảng giá trị sau:ii) Trong mặt phẳng toạ độ \(Oxy\), xác định các điểm có toạ độ như bảng trên. Làm tương tự, lấy nhiều điểm \(M\left( {x;{{\log }_2}x} \right)\) với \(x > 0\) và nối lại ta được đồ thị hàm số \(y = {\log _2}x\) như Hình 4. Từ đồ thị này, nêu nhận xét về tính liên tục, tính đồng biến, nghịch...
Đọc tiếp

a) Xét hàm số \(y = {\log _2}x\) với tập xác định \(D = \left( {0; + \infty } \right)\).

i) Hoàn thành bảng giá trị sau:

ii) Trong mặt phẳng toạ độ \(Oxy\), xác định các điểm có toạ độ như bảng trên. Làm tương tự, lấy nhiều điểm \(M\left( {x;{{\log }_2}x} \right)\) với \(x > 0\) và nối lại ta được đồ thị hàm số \(y = {\log _2}x\) như Hình 4. Từ đồ thị này, nêu nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi \(x \to  + \infty ,x \to {0^ + }\) và tập giá trị của hàm số đã cho.

b) Lập bảng giá trị và vẽ đồ thị của hàm số \(y = {\log _{\frac{1}{2}}}x\). Từ đó, nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi \(x \to  + \infty ,x \to {0^ + }\) và tập giá trị của hàm số này.
#Toán lớp 11
1
NL
Nguyễn Lê Phước Thịnh
21 tháng 8 2023

a:

i: 

x1/2124
y-1012

 

ii:

Hàm số liên tục và đồng biến trên \(\left(0;+\infty\right)\)

\(\lim\limits_{x\rightarrow+\infty}log_2x=+\infty;\lim\limits_{x\rightarrow0^+}log_2x=-\infty\)

Tập giá trị: R

b:

x1/2124
y10-1-2

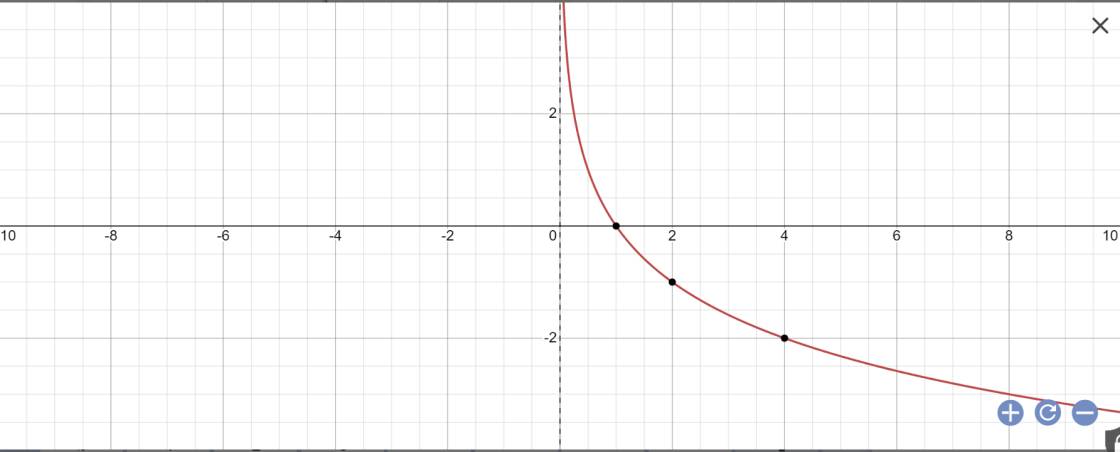
loading...

Hàm số liên tục và nghịch biến trên \(\left(0;+\infty\right)\)

\(\lim\limits_{x\rightarrow+\infty}log_{\dfrac{1}{2}}x=-\infty;\lim\limits_{x\rightarrow0^+}log_{\dfrac{1}{2}}x=+\infty\)

Tập giá trị: R

Đúng(0)
B
Buddy
15 tháng 8 2023
Cho hàm số mũ \(y = {2^x}.\)a) Hoàn thành bảng giá trị sau:b) Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; 2x) với \(x \in \mathbb{R}\) và nối lại ta được đồ thị của hàm sốc) Từ đồ thị đã vẽ ở câu b, hãy kết luận về tập giá trị và tính chất biến thiên của hàm...
Đọc tiếp

Cho hàm số mũ \(y = {2^x}.\)

a) Hoàn thành bảng giá trị sau:

b) Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; 2x) với \(x \in \mathbb{R}\) và nối lại ta được đồ thị của hàm số

c) Từ đồ thị đã vẽ ở câu b, hãy kết luận về tập giá trị và tính chất biến thiên của hàm số
#Toán lớp 11
1
HQ
Hà Quang Minh
Giáo viên
25 tháng 8 2023

Đúng(0)
B
Buddy
13 tháng 8 2023
Cho hàm số lôgarit \(y = {\log _{\frac{1}{2}}}x\)a)     Tìm giá trị y tương ứng với giá trị của x trong bảng sau:b,    Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a.Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;{{\log }_{\frac{1}{2}}}x} \right)\) với \(x \in (0; + \infty )\) và nối lại ta được đồ thị hàm số \(y = {\log _{\frac{1}{2}}}x\) như hình bên.c,   Cho biết tọa độ giao...
Đọc tiếp

Cho hàm số lôgarit \(y = {\log _{\frac{1}{2}}}x\)

a)     Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

b,    Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a.

Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;{{\log }_{\frac{1}{2}}}x} \right)\) với \(x \in (0; + \infty )\) và nối lại ta được đồ thị hàm số \(y = {\log _{\frac{1}{2}}}x\) như hình bên.

c,   Cho biết tọa độ giao điểm của đồ thị hàm số \(y = {\log _{\frac{1}{2}}}x\) với trục hoành và vị trí của đồ thị hàm số đó với trục tung.

d,     Quan sát đồ thị hàm số \(y = {\log _{\frac{1}{2}}}x\), nêu nhận xét về:

\(\mathop {\lim }\limits_{x \to {0^ + }} ({\log _{\frac{1}{2}}}x)\,;\mathop {\,\,\mathop {\lim }\limits_{x \to  + \infty } ({{\log }_{\frac{1}{2}}}x)}\limits_{} \)Sự biến thiên của hàm số \(y = {\log _{\frac{1}{2}}}x\) và lập bảng biến thiên của hàm số đó.
#Toán lớp 11
1
NL
Nguyễn Lê Phước Thịnh
22 tháng 9 2023

a: 

x0,51248
\(y\)-10123

b:

c: Tọa độ giao điểm của hàm số với trục hoành là B(2;0)

Đồ thị hàm số này ko cắt trục tung

d: 

\(\lim\limits_{x\rightarrow0^+}log_2x=0\)

\(\lim\limits_{x\rightarrow+\infty}\left(log_2x\right)=+\infty\)

=>Hàm số này đồng biến trên TXĐ của nó là D=[0;+vô cực)

Đúng(0)
B
Buddy
15 tháng 8 2023

Cho đồ thị của hàm số \(y = {\log _2}x\) và y = 2 như Hình 6.8. Tìm khoảng giá trị của x mà đồ thị hàm số \(y = {\log _2}x\) nằm phía trên đường thẳng y = 2 và từ đó suy ra tập nghiệm của bất phương trình \({\log _2}x > 2.\)
#Toán lớp 11
1
HQ
Hà Quang Minh
Giáo viên
24 tháng 8 2023

Khoảng giá trị của x mà đồ thị hàm số \(y=log_2x\) nằm phía trên đường thẳng y = 2 là \(\left(4;+\infty\right)\)

\(\Rightarrow\) Tập nghiệm của bất phương trình \(log_2x>2\) là \(\left(4;+\infty\right)\)

Đúng(0)
B
Buddy
13 tháng 8 2023
Cho hàm số mũ \(y = {2^x}\)a)     Tìm giá trị y tương ứng với giá trị của x trong bảng sau:b)    Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm trong bảng giá trị ở câu a.Bằng cách tương tự, lấy nhiều điểm \(\left( {x;{2^x}} \right)\) với \(x \in \mathbb{R}\) và nối lại, ta được đồ thị hàm số \(y = {2^x}\) (Hình 1)c)     Cho biết tọa độ giao điểm của đồ thị hàm số \(y = {2^x}\) với trục tung và vị...
Đọc tiếp

Cho hàm số mũ \(y = {2^x}\)

a)     Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

b)    Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm trong bảng giá trị ở câu a.

Bằng cách tương tự, lấy nhiều điểm \(\left( {x;{2^x}} \right)\) với \(x \in \mathbb{R}\) và nối lại, ta được đồ thị hàm số \(y = {2^x}\) (Hình 1)

c)     Cho biết tọa độ giao điểm của đồ thị hàm số \(y = {2^x}\) với trục tung và vị trí của đồ thị hàm số đó so với trục hoành.

d)    Quan sát đồ thị hàm số \(y = {2^x}\), nêu nhận xét về:

\(\mathop {\lim {2^x}}\limits_{x \to  + \infty } ;\,\mathop {\lim {2^x}}\limits_{x \to  - \infty } \)Sự biến thiên của hàm số \(y = {2^x}\) và lập bảng biến thiên của hàm số đó.
#Toán lớp 11
2
NL
Nguyễn Lê Phước Thịnh
22 tháng 9 2023

a: 

x-10123
y\(\dfrac{1}{2}\)1248

b: Tham khảo:

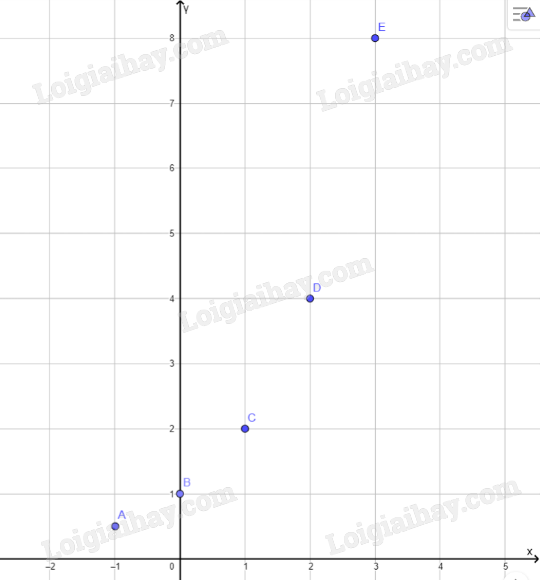
c: Tọa độ giao điểm của hàm số với trục tung là B(0;1)

Đồ thị hàm số này ko cắt trục hoành

d: 

\(\lim\limits_{x\rightarrow+\infty}2^x=+\infty;\lim\limits_{x\rightarrow-\infty}2^x=+\infty\)

=>Hàm số này đồng biến trên R

Bảng biến thiên:

Đúng(1)
MT
Mai Trung Hải Phong
22 tháng 9 2023

tham khảo

loading...

b)    Biểu diễn các điểm ở câu a:

loading...

Đúng(0)
B
Buddy
15 tháng 8 2023

a) Tính \(y = {\log _2}x\) khi x lần lượt nhận các giá trị 1; 2; 4. Với mỗi giá trị của x > 0 có bao nhiêu giá trị của \(y = {\log _2}x\) tương ứng?

b) Với những giá trị nào của x, biểu thức \(y = {\log _2}x\) có nghĩa?
#Toán lớp 11
1
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023

a) Với \(x = 1\) thì \(y = {\log _2}1 = 0\)

Với \(x = 2\) thì \(y = {\log _2}2 = 1\)

Với \(x = 4\) thì \(y = {\log _2}4 = 2\)

b) Biểu thức \(y = {\log _2}x\) có nghĩa khi x > 0.

Đúng(0)
B
Buddy
13 tháng 8 2023
Hoạt động 3Cho hàm số mũ \(y = {\left( {\frac{1}{2}} \right)^x}\)a)     Tìm giá trị y tương ứng với giá trị của x trong bảng sau:b,     Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm trong bảng giá trị ở câu a.Bằng cách tương tự, lấy nhiều điểm \(\left( {x;{{\left( {\frac{1}{2}} \right)}^x}} \right)\) với \(x \in \mathbb{R}\) và nối lại, ta được đồ thị hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) (Hình 2)c,   Cho...
Đọc tiếp

Hoạt động 3

Cho hàm số mũ \(y = {\left( {\frac{1}{2}} \right)^x}\)

a)     Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

b,     Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm trong bảng giá trị ở câu a.

Bằng cách tương tự, lấy nhiều điểm \(\left( {x;{{\left( {\frac{1}{2}} \right)}^x}} \right)\) với \(x \in \mathbb{R}\) và nối lại, ta được đồ thị hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) (Hình 2)

c,   Cho biết tọa độ giao điểm của đồ thị hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) với trục tung và vị trí của đồ thị hàm số đó so với trục hoành.

d,     Quan sát đồ thị hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\), nêu nhận xét về:

\(\mathop {\lim {{\left( {\frac{1}{2}} \right)}^x}}\limits_{x \to  + \infty } ;\,\mathop {\lim {{\left( {\frac{1}{2}} \right)}^x}}\limits_{x \to  - \infty } \)Sự biến thiên của hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) và lập bảng biến thiên của hàm số đó.
#Toán lớp 11
1
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023

a)     \(y = {\left( {\frac{1}{2}} \right)^x}\)

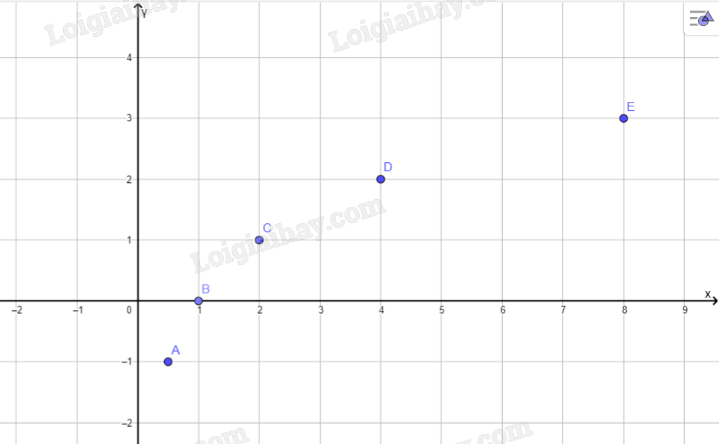
a)     Biểu diễn các điểm ở câu a:

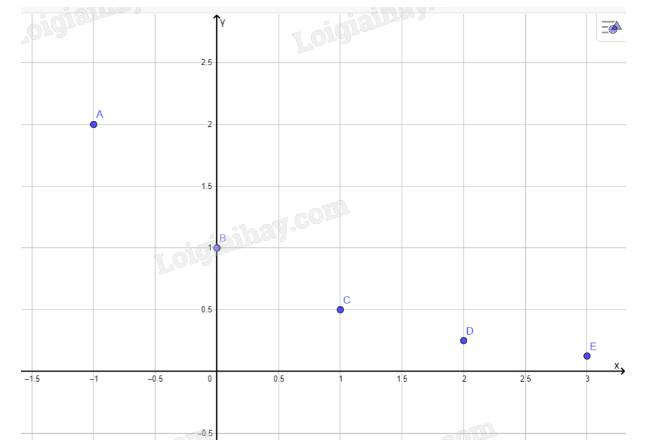
b)    Tọa độ giao điểm của đồ thị hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) với trục tung là (0;1)

Đồ thị hàm số đó không cắt trục hoành

c)     \(\mathop {\lim }\limits_{x \to  + \infty } {\left( {\frac{1}{2}} \right)^x} = 0;\,\,\mathop {\lim }\limits_{x \to  - \infty } {\left( {\frac{1}{2}} \right)^x} =  + \infty \)

Hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) nghịch biến trên toàn  \(\mathbb{R}\)

Bảng biến thiên của hàm số:

Đúng(0)
B
Buddy
13 tháng 8 2023

Hoạt động 6

Quan sát Hình 12 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số lôgarit \(y = {\log _2}x\). Từ đó, hãy tìm x sao cho \({\log _2}x > 1\)
#Toán lớp 11
1
HQ
Hà Quang Minh
Giáo viên
22 tháng 8 2023

Do 2 > 1 ⇒ hàm số y = log2x đồng biến trên D = \(\left(0;+\infty\right)\)

\(log_2x>1\\ \Rightarrow x>2\)

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP