Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(I=\int\limits^1_0x.f\left(3x\right)dx\)
Đặt \(3x=u\Rightarrow dx=\dfrac{1}{3}du\) ; \(\left\{{}\begin{matrix}x=0\Rightarrow u=0\\x=1\Rightarrow u=3\end{matrix}\right.\)
\(\Rightarrow I=\dfrac{1}{9}\int\limits^3_0u.f\left(u\right)du=\dfrac{1}{9}\int\limits^3_0x.f\left(x\right)dx=1\)
\(\Rightarrow J=\int\limits^3_0x.f\left(x\right)dx=9\)
Xét J, đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=x.dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=\dfrac{x^2}{2}\end{matrix}\right.\)
\(\Rightarrow J=\dfrac{x^2}{2}.f\left(x\right)|^3_0-\dfrac{1}{2}\int\limits^3_0x^2.f'\left(x\right)dx=\dfrac{9}{2}-\dfrac{1}{2}\int\limits^3_0x^2.f'\left(x\right)dx\)
\(\Rightarrow\int\limits^3_0x^2.f'\left(x\right)dx=9-2J=-9\)

Chọn C.
Đặt u = G ( x ) d v = f ( x ) d x ⇒ d u = G ( x ) ' d x = g ( x ) d x v = ∫ f ( x ) d x = F ( x )
Suy ra: I = G ( x ) F ( x ) 2 0 - ∫ 0 2 F ( x ) g ( x ) d x
= G(2)F(2) – G(0)F(0) – 3 = 1 – 0 – 3 = -2.

Theo bất đẳng thức Cauchy-Schwarz cho tích phân có:
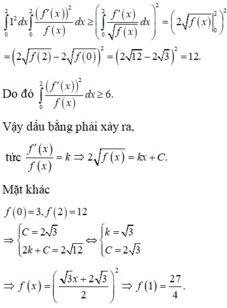
Đáp án A
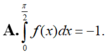
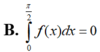
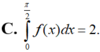
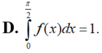
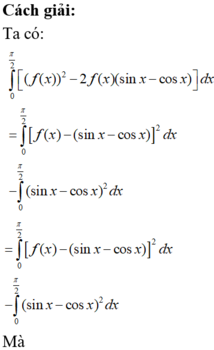

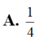
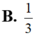

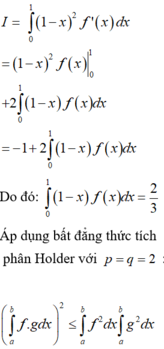
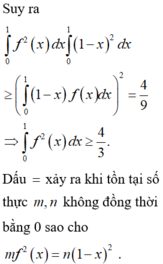
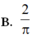
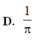
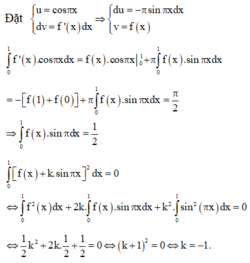
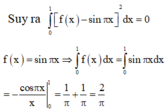
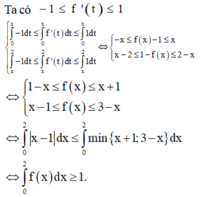

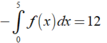
Đề là cho \(\int\limits^{\dfrac{\pi}{2}}_0sin2x.f\left(cos^2x\right)dx=1\)
Tính \(\int\limits^1_0\left[2f\left(1-x\right)-3x^2+5\right]dx\)
Đúng ko nhỉ?
Xét \(\int\limits^{\dfrac{\pi}{2}}_0sin2x.f\left(cos^2x\right)dx\)
Đặt \(cos^2x=1-u\Rightarrow-2sinx.cosxdx=-du\) \(\Rightarrow sin2xdx=du\)
\(\left\{{}\begin{matrix}x=0\Rightarrow u=0\\x=\dfrac{\pi}{2}\Rightarrow u=1\end{matrix}\right.\) \(\Rightarrow I=\int\limits^1_0f\left(1-u\right)du=\int\limits^1_0f\left(1-x\right)dx\)
\(\Rightarrow\int\limits^1_0f\left(1-x\right)dx=1\)
\(\Rightarrow\int\limits^1_0\left[2f\left(1-x\right)-3x^2+5\right]dx=2\int\limits^1_0f\left(1-x\right)dx-\int\limits^1_0\left(3x^2-5\right)dx\)
\(=2.1-\left(-4\right)=6\)
Có thể giải thích chỗ đặt đc ko ạ