Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\lim\limits_{x\rightarrow-1^-}f\left(x\right)=2-a+b\)
\(\lim\limits_{x\rightarrow-1^+}f\left(x\right)=-4+2a\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=4+2a\)
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=a+b\)
Để hs có giới hạn tại \(x=1;-1\) thì:
\(\left\{{}\begin{matrix}2-a+b=-4+2a\\4+2a=a+b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3a-b=2\\a-b=-4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=3\\b=7\end{matrix}\right.\)

\(\lim\limits_{x\rightarrow2}f\left(x\right)=\lim\limits_{x\rightarrow2}\dfrac{2-\sqrt{2x^2-4}}{2-x}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{4-2x^2+4}{2+\sqrt{2x^2-4}}\cdot\dfrac{1}{2-x}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{-2\left(x^2-4\right)}{-\left(x-2\right)\left(2+\sqrt{2x^2-4}\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{2\left(x-2\right)\left(x+2\right)}{\left(x-2\right)\left(2+\sqrt{2x^2-4}\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{2\left(x+2\right)}{2+\sqrt{2x^2-4}}=\dfrac{2\left(2+2\right)}{2+\sqrt{2\cdot2^2-4}}\)
\(=\dfrac{2\cdot4}{2+2}=\dfrac{8}{4}=2\)
\(f\left(2\right)=1\)
=>\(\lim\limits_{x\rightarrow2}f\left(x\right)< >f\left(2\right)\)
=>Hàm số bị gián đoạn tại x=2

\(\lim\limits_{x\rightarrow2}f\left(x\right)=\lim\limits_{x\rightarrow2}\dfrac{2x^2-7x+6}{2-x}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{2x^2-4x-3x+6}{-\left(x-2\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(3-2x\right)}{x-2}=\lim\limits_{x\rightarrow2}3-2x=3-2\cdot2=3-4=-1\)
\(f\left(2\right)=2\cdot2-5=-1\)
=>\(\lim\limits_{x\rightarrow2}f\left(x\right)=f\left(2\right)\)
=>Hàm số liên tục tại x=2

\(\lim\limits_{x\rightarrow2}f\left(x\right)=\lim\limits_{x\rightarrow2}\dfrac{x^2-4}{2-x}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+2\right)}{-\left(x-2\right)}=\lim\limits_{x\rightarrow2}-\left(x+2\right)\)
\(=-\left(2+2\right)=-4\)
\(f\left(2\right)=2-7=-5\)
=>\(\lim\limits_{x\rightarrow2}f\left(x\right)< >f\left(2\right)\)
=>Hàm số gián đoạn tại x=2
Khi \(x\ne\)2 thì \(f\left(x\right)=\dfrac{x^2-4}{2-x}\) hoàn toàn xác định nên hàm số liên tục trên các khoảng \(\left(-\infty;2\right);\left(2;+\infty\right)\)

\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}x^2+3x+1=1+3\cdot1+1=5\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}2x+2=2\cdot1+2=4\)
f(1)=1+3+1=5
=>\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=f\left(1\right)\ne\lim\limits_{x\rightarrow1^-}f\left(x\right)\)
=>Hàm số bị gián đoạn tại x=1

Đề lỗi công thức toán rồi bạn. Không nhìn thấy được biểu thức hiển thị.

\(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\dfrac{2x^2-5x+3}{x-1}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(2x-3\right)}{x-1}=\lim\limits_{x\rightarrow1}2x-3=2\cdot1-3=-1\)
f(1)=4
=>\(\lim\limits_{x\rightarrow1}f\left(x\right)< >f\left(1\right)\)
=>Hàm số bị gián đoạn tại x=1

\(\lim\limits_{x\rightarrow5}f\left(x\right)=\lim\limits_{x\rightarrow5}\dfrac{x^2-8x+15}{x-5}\)
\(=\lim\limits_{x\rightarrow5}\dfrac{\left(x-3\right)\left(x-5\right)}{x-5}=\lim\limits_{x\rightarrow5}x-3=5-3=2\)
f(5)=2*5-1=9
=>\(f\left(5\right)\ne\lim\limits_{x\rightarrow5}f\left(x\right)\)
=>Hàm số gián đoạn tại x=5


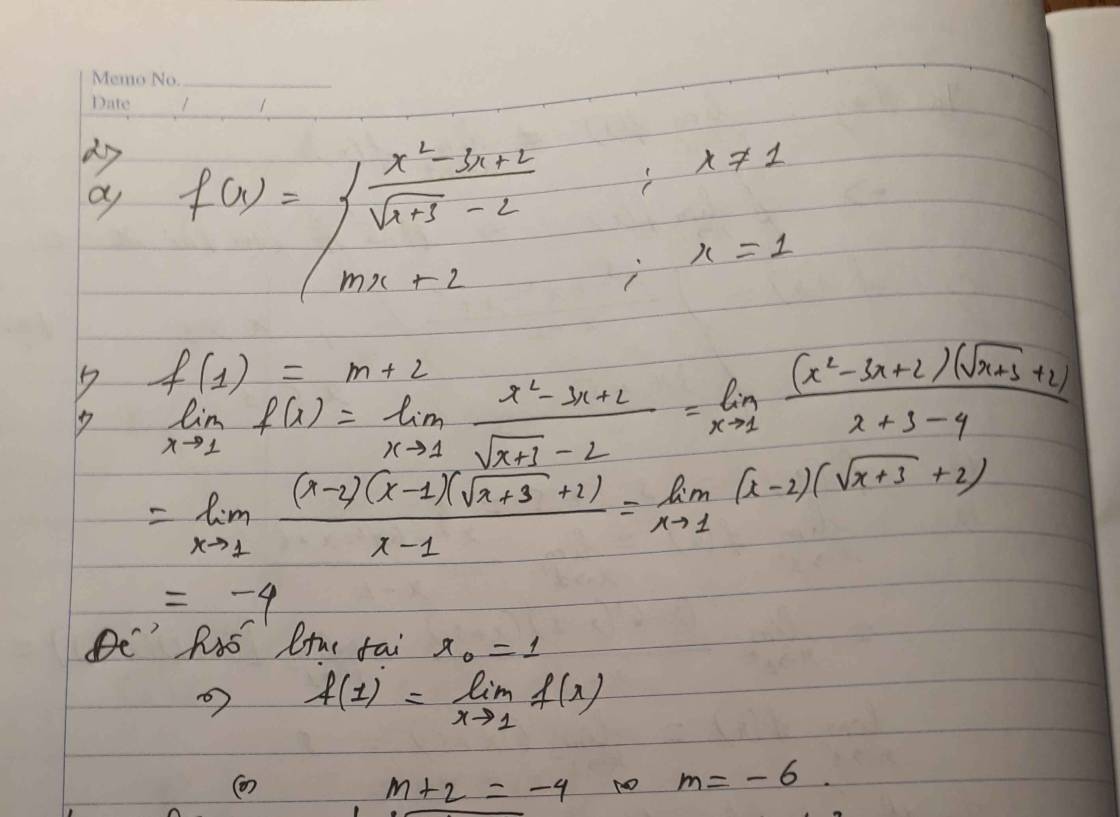
\(\lim\limits_{x\rightarrow-2}f\left(x\right)=\lim\limits_{x\rightarrow-2}\frac{x+2}{\left(x+2\right)\left(x-4\right)}=\lim\limits_{x\rightarrow-2}\frac{1}{x-4}=-\frac{1}{6}\)
\(f\left(-2\right)=-2a+1\)
Để hàm số liên tục (chứ ko phải có giới hạn) tại \(x=-2\) thì:
\(\lim\limits_{x\rightarrow-2}f\left(x\right)=f\left(-2\right)\Leftrightarrow-2a+1=-\frac{1}{6}\Rightarrow a=\frac{7}{12}\)
Bạn ghi sai đề, chắc chắn
Đầu tiên 2 biểu thức của \(f\left(x\right)\) ko liên quan đến nhau, nếu dòng đầu là \(x\ne2\) thì dòng 2 phải là \(x=2\), hoặc ngược lại
Tiếp theo, hàm số ko hề bị gián đoạn tại \(x=1\) (chẳng liên quan gì tới số 1 ở đây) nên chắc chắn hàm luôn có giới hạn tại \(x=1\) ko phụ thuộc vào tham số a