OLM cung cấp gói bải giảng điện tử PPT cho giáo viên đầu năm học

Thi thử và xem hướng dẫn giải chi tiết đề tham khảo 12 môn thi Tốt nghiệp THPT 2025

Tham gia cuộc thi "Nhà giáo sáng tạo" ẫm giải thưởng với tổng giá trị lên đến 10 triệu VNĐ

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
B
Buddy
17 tháng 7 2023
Cho hai hàm số  và \(y = g\left( x \right) = \frac{x}{{x + 1}}\).a) Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thoả mãn \({x_n} \ne  - 1\) với mọi \(n\) và \({x_n} \to 1\) khi \(n \to  + \infty \). Tìm giới hạn \(\lim \left[ {f\left( {{x_n}} \right) + g\left( {{x_n}} \right)} \right]\).b) Từ đó, tìm giới hạn \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right]\), và so sánh với \(\mathop {\lim }\limits_{x \to 1} {\rm{...
Đọc tiếp

Cho hai hàm số  và \(y = g\left( x \right) = \frac{x}{{x + 1}}\).

a) Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thoả mãn \({x_n} \ne  - 1\) với mọi \(n\) và \({x_n} \to 1\) khi \(n \to  + \infty \). Tìm giới hạn \(\lim \left[ {f\left( {{x_n}} \right) + g\left( {{x_n}} \right)} \right]\).

b) Từ đó, tìm giới hạn \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right]\), và so sánh với \(\mathop {\lim }\limits_{x \to 1} {\rm{ }}f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right)\).
#Toán lớp 11
1
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023

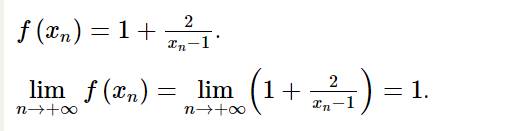
a) \(\lim \left[ {f\left( {{x_n}} \right) + g\left( {{x_n}} \right)} \right] = \lim \left( {2{x_n} + \frac{{{x_n}}}{{{x_n} + 1}}} \right) = 2\lim {x_n} + \lim \frac{{{x_n}}}{{{x_n} + 1}} = 2.1 + \frac{1}{{1 + 1}} = \frac{5}{2}\)

b) Vì \(\lim \left[ {f\left( {{x_n}} \right) + g\left( {{x_n}} \right)} \right] = \frac{5}{2}\) nên \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right] = \frac{5}{2}\) (1).

Ta có:   \(\lim {\rm{ }}f\left( {{x_n}} \right) = \lim 2{x_n} = 2\lim {x_n} = 2.1 = 2 \Rightarrow \mathop {\lim }\limits_{x \to 1} {\rm{ }}f\left( x \right) = 2\)

\(\lim g\left( {{x_n}} \right) = \lim \frac{{{x_n}}}{{{x_n} + 1}} = \lim \frac{{{x_n}}}{{{x_n} + 1}} = \frac{1}{{1 + 1}} = \frac{1}{2} \Rightarrow \mathop {\lim }\limits_{x \to 1} {\rm{ }}g\left( x \right) = \frac{1}{2}\)

Vậy \(\mathop {\lim }\limits_{x \to 1} {\rm{ }}f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right) = 2 + \frac{1}{2} = \frac{5}{2}\) (2).

Từ (1) và (2) suy ra \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} {\rm{ }}f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right)\)

Đúng(0)
MA
Mai Anh
14 tháng 4 2022
Cho hàm số y=f(x) xác định trên (a;b). Nếu \(\forall\left(x_o\right),x_n\ne x_o,l\text{imx}_n=x_o\Rightarrow...
Đọc tiếp

Cho hàm số y=f(x) xác định trên (a;b). Nếu \(\forall\left(x_o\right),x_n\ne x_o,l\text{imx}_n=x_o\Rightarrow l\text{imf}\left(x_n\right)=+\infty\) thì:

A. \(\lim\limits_{x->x_o}f\left(x\right)=L\)

B. \(\lim\limits_{x->x_o^-}f\left(x\right)=-\infty\)

C. \(\lim\limits_{x->x_o}f\left(x\right)=-\infty\)

D. \(\lim\limits_{x->x_o}f\left(x\right)=+\infty\)
#Toán lớp 11
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022

\(\lim\limits_{x\rightarrow x_0}f\left(x\right)=+\infty\)

Đúng(0)
LS
Lê Song Phương
29 tháng 7 2023 - olm
Câu hỏi hay

 Cho dãy số \(\left(x_n\right)^{+\infty}_{n=1}\) như sau: \(x_1=a>2\) và 

\(x_{n+1}=x_n^2-2,\forall n=1,2,...\)

 Tìm \(\lim\limits_{n\rightarrow+\infty}\left(\dfrac{1}{x_1}+\dfrac{1}{x_1x_2}+\dfrac{1}{x_1x_2x_3}+...+\dfrac{1}{x_1x_2...x_n}\right)\)
#Toán lớp 11
2
ND
Nguyễn Đức Trí
30 tháng 7 2023

\(x_1=a>2;x_{n+1}=x_n^2-2,\forall n=1,2,...\)

mà \(n\rightarrow+\infty\)

\(\Rightarrow a\rightarrow+\infty\Rightarrow x_n\rightarrow+\infty\)

\(\Rightarrow\lim\limits_{n\rightarrow+\infty}\dfrac{1}{x_n}=0\) \(\Rightarrow\lim\limits_{n\rightarrow+\infty}\left(\dfrac{1}{x_nx_{n+1}}\right)=0\)

\(\)\(\Rightarrow\lim\limits_{n\rightarrow+\infty}\left(\dfrac{1}{x_1}+\dfrac{1}{x_1x_2}+\dfrac{1}{x_1x_2x_3}+...+\dfrac{1}{x_1x_2...x_n}\right)=0\)

Đúng(2)
DN
Đặng Ninh Phượng
31 tháng 7 2023

...

 

 

 

Đúng(0)
MA
Mai Anh
13 tháng 4 2022

Cho hàm số \(f\left(x\right)=2x-3\)   và dãy số \(\left(x_n\right)\) , lim \(x_n=1\)  . Tính \(limf\left(x_n\right)\)
#Toán lớp 11
0
MA
Mai Anh
14 tháng 4 2022

Cho hàm số \(f\left(x\right)=2x-3\)   và dãy số \(\left(x_n\right)\) , lim \(x_n=1\)  . Tính \(limf\left(x_n\right)\)
#Toán lớp 11
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022

\(\lim\limits f\left(x_n\right)=f\left(1\right)=-1\)

Đúng(0)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
Xét hàm số \(f\left( x \right) = 2x.\)a) Xét dãy số \(\left( {{x_n}} \right),\) với \({x_n} = 1 + \frac{1}{n}.\) Hoàn thành bảng giá trị \(f\left( {{x_n}} \right)\) tương ứng.Các giá trị tương ứng của hàm số \(f\left( {{x_1}} \right),f\left( {{x_2}} \right),...,f\left( {{x_n}} \right),...\) lập thành một dãy số mà ta kí hiệu là \(\left( {f\left( {{x_n}} \right)} \right).\) Tìm \(\lim f\left( {{x_n}} \right).\)b) Chứng minh rằng với dãy số bất kì...
Đọc tiếp

Xét hàm số \(f\left( x \right) = 2x.\)

a) Xét dãy số \(\left( {{x_n}} \right),\) với \({x_n} = 1 + \frac{1}{n}.\) Hoàn thành bảng giá trị \(f\left( {{x_n}} \right)\) tương ứng.

Các giá trị tương ứng của hàm số \(f\left( {{x_1}} \right),f\left( {{x_2}} \right),...,f\left( {{x_n}} \right),...\) lập thành một dãy số mà ta kí hiệu là \(\left( {f\left( {{x_n}} \right)} \right).\) Tìm \(\lim f\left( {{x_n}} \right).\)

b) Chứng minh rằng với dãy số bất kì \(\left( {{x_n}} \right),{x_n} \to 1\) ta luôn có \(f\left( {{x_n}} \right) \to 2.\)
#Toán lớp 11
1
KS
Kiều Sơn Tùng
22 tháng 9 2023

Tham khảo:

a,

\(\lim f\left( {{x_n}} \right) = \lim \left( {2.\frac{{n + 1}}{n}} \right) = \lim 2.\lim \left( {1 + \frac{1}{n}} \right) = 2.\left( {1 + 0} \right) = 2\)

b) Lấy dãy số bất kì \(\left( {{x_n}} \right),{x_n} \to 1\) ta có \(f\left( {{x_n}} \right) = 2{x_n}.\)

 \(\lim f\left( {{x_n}} \right) = \lim \left( {2{x_n}} \right) = \lim 2.\lim {x_n} = 2.1 = 2\)

Đúng(0)
LS
Lê Song Phương
1 tháng 8 2023 - olm
Câu hỏi hay
 Xét dãy số \(\left\{x_n\right\}^{+\infty}_{n=1}\) như sau: \(x_1=1\) và với mọi \(n=1,2,...\) thì  \(x_{n+1}=\dfrac{\left(2+\cos\alpha\right)x_n+\cos^2\alpha}{\left(2-2\cos2\alpha\right)x_n+2-2\cos2\alpha}\), trong đó \(\alpha\) là một tham số thực. Tìm tất cả các giá trị của \(\alpha\) để dãy số \(\left\{y_n\right\}\), với \(y_n=\sum\limits^n_{k=1}\dfrac{1}{2x_k+1},\forall n=1,2,...\) có giới hạn hữu hạn khi \(n\rightarrow+\infty\). Hãy tìm giới hạn...
Đọc tiếp

 Xét dãy số \(\left\{x_n\right\}^{+\infty}_{n=1}\) như sau: \(x_1=1\) và với mọi \(n=1,2,...\) thì 

\(x_{n+1}=\dfrac{\left(2+\cos\alpha\right)x_n+\cos^2\alpha}{\left(2-2\cos2\alpha\right)x_n+2-2\cos2\alpha}\),

trong đó \(\alpha\) là một tham số thực. Tìm tất cả các giá trị của \(\alpha\) để dãy số \(\left\{y_n\right\}\), với \(y_n=\sum\limits^n_{k=1}\dfrac{1}{2x_k+1},\forall n=1,2,...\) có giới hạn hữu hạn khi \(n\rightarrow+\infty\). Hãy tìm giới hạn của dãy số \(\left\{y_n\right\}\) trong các trường hợp đó.
#Toán lớp 11
3
MD
Mạnh Dũng
1 tháng 8 2023

1e+84937

Đúng(1)
TD
Thành Đông Phạm
4 tháng 8 2023

Ta có xn luôn dương

Ta có \(2x_n+1=\) \(2\times\dfrac{\left(2+cos\alpha\right)x_n+cos^2\alpha}{\left(2-2cos2\alpha\right)x_n+2-cos2\alpha}+1=\)

\(=\dfrac{6x_n+2cos^2\alpha+2-cos2\alpha}{\left(2-2cos2\alpha\right)x_n+2-cos2\alpha}\)

\(=\dfrac{6x_n+2cos^2\alpha+2sin^2a+1}{\left(2x_n+1\right)\left(1-cos2\alpha\right)+1}\)

\(=\dfrac{3\left(2x_n+1\right)}{2\sin^2\alpha\left(2x_n+1\right)+1}\)

\(\Rightarrow\dfrac{1}{2x_{n+1}+1}=\dfrac{2\sin^2\alpha\left(2x_n+1\right)+1}{3\left(2x_n+1\right)}\)

\(=\dfrac{1}{3}\left(2\sin^2\alpha+\dfrac{1}{2x_n+1}\right)\)

\(\Rightarrow\dfrac{1}{2x_{n+1}+1}-\sin^2\alpha=\dfrac{1}{3}\left(\dfrac{1}{2x_n+1}-\sin^2\alpha\right)\)

\(\Rightarrow\dfrac{1}{2x_{n+1}+1}-\sin^2\alpha=\left(\dfrac{1}{3}\right)^n\left(\dfrac{1}{2x_1+1}-\sin^2\alpha\right)\)

\(=\left(\dfrac{1}{3}\right)^n\left(\dfrac{1}{3}-\sin^2\alpha\right)\)

\(\Rightarrow y_n=\sum\limits^{n-1}_{i=0}\left(\dfrac{1}{3}\right)^i\left(\dfrac{1}{3}-\sin^2\alpha\right)+n\sin^2\alpha\)

\(=\dfrac{1-\left(\dfrac{1}{3}\right)^n}{1-\dfrac{1}{3}}\left(\dfrac{1}{3}-\sin^2\alpha\right)+n\sin^2\alpha\)

Đúng(1)
SG
Sách Giáo Khoa
11 tháng 4 2017

Tính giới hạn \(\lim\limits_{n\rightarrow+\infty}x_n\) :

a) \(x_n=\dfrac{\sqrt{n^2+1}+\sqrt{n}}{\sqrt[3]{n^3+n}-n}\)

b) \(x_n\left(n-\dfrac{1}{n}\right)\left(\dfrac{1-4n}{2n^2}\right)\)
#Toán lớp 11
0
NT
Nguyễn Thu Ngà
29 tháng 3 2021

\(\left\{{}\begin{matrix}x_1=1\\x_{n+1}=\sqrt{x_n\left(x_n+1\right)\left(x_n+2\right)\left(x_n+3+1\right)}\end{matrix}\right.\). Đặt \(\dfrac{y_n}{x_n}=\sum\limits^n_{i=1}\dfrac{1}{x_i+2}\). Tìm lim \(y_n\)
#Toán lớp 11
1
E
Etermintrude💫
30 tháng 3 2021

undefined

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP