Cho hàm số f x = x , x o = 4 và Δ x = 0 , 01 . Tính f ’ ( x o )...

Cho hàm số f x = x , x o = 4 và Δ x...

ND

Nho Dora

21 tháng 4 2022

cho hàm số y=f(x)=-x³+2x²-x+5 có đồ thị (C). Tìm tham số m để tiếp tuyến Δ của đồ thị (C) tại tiếp điểm A(2;3) song song với đường thẳng (d): (m²-3m-5)x-y-2m+19=0

#Toán lớp 11

1

NV

Nguyễn Việt Lâm

Giáo viên

23 tháng 4 2022

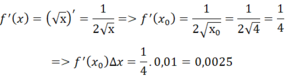
\(\left(m^2-3m-5\right)x-y-2m+19=0\)

\(\Leftrightarrow y=\left(m^2-3m-5\right)x-2m+19\)

Ta có:

\(f'\left(x\right)=-3x^2+4x-1\)

\(f'\left(2\right)=-5\)

Phương trình tiếp tuyến tại A:

\(y=-5\left(x-2\right)+3\Leftrightarrow y=-5x+13\)

Để hai đường thẳng song song:

\(\Leftrightarrow\left\{{}\begin{matrix}m^2-3m-5=-5\\-2m+19\ne13\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m^2-3m=0\\2m\ne6\end{matrix}\right.\)

\(\Leftrightarrow m=0\)

Đúng(0)

PT

Pham Trong Bach

23 tháng 12 2019

Trong Oxy, cho phép biến hình F biến mỗi điểm M(x;y) thành điểm M’(x’;y’) thỏa mãn . Phép biến hình F biến đt Δ : 2x + 3y + 3 = 0 thành đt (d) có phương trình: A. 1 12 x − 10 3 = y B. − 1 12 x − 10 3 = y C. 1 12 x − 10 3 = − y D. 1 12 x + 10 3 = y ...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

23 tháng 12 2019

Đáp án A

Chọn A(–3; 1) ⇒ F ( A ) = A ' ( − 8 ; − 4 )

B(3;–3) ⇒ F ( B ) = B ' ( 16 ; − 2 )

Phương trình đường thẳng (d) đi qua 2 điểm A’, B’: 1 12 x − 10 3 = y

Đúng(0)

BN

Bùi Ngọc Yến Nhi

14 tháng 4 2021

Cho hàm số f(x)=1/2sin2x-cosx-x+2015.Tính f'(x) và tìm x để f'(x)=0

#Toán lớp 11

1

NV

Nguyễn Việt Lâm

Giáo viên

15 tháng 4 2021

Đề là \(f\left(x\right)=\dfrac{1}{2}sin2x-cosx-x+2015\) đúng không nhỉ?

\(f'\left(x\right)=cos2x+sinx-1\)

\(f'\left(x\right)=0\Leftrightarrow cos2x+sinx-1=0\)

\(\Leftrightarrow1-2sin^2x+sinx-1=0\)

\(\Leftrightarrow sinx\left(1-2sinx\right)=0\Rightarrow\left[{}\begin{matrix}sinx=0\\sinx=\dfrac{1}{2}\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)

Đúng(1)

HH

hằng hồ thị hằng

10 tháng 4 2021

1, Cho hàm số y=f(x) và f'(0)=3. Hỏi giới hạn \(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x+1}-1}{f\left(0\right)-f\left(x\right)}\)=?2, Cho hàm số f(x) có đạo hàm trên R và f'(x)=0 có các nghiệm là 1 và -2. Đặt \(g\left(x\right)=f\left(\sqrt{x^2+4}\right)\), hỏi g'(x)=0 có bao nhiêu nghiệm?Mọi người giúp mình với ạ, mình cần gấp!! Cảm ơn mọi người rất...

Đọc tiếp

#Toán lớp 11

1

NV

Nguyễn Việt Lâm

Giáo viên

10 tháng 4 2021

1. Áp dụng quy tắc L'Hopital

\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x+1}-1}{f\left(0\right)-f\left(x\right)}=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{1}{2\sqrt{x+1}}}{-f'\left(0\right)}=-\dfrac{1}{6}\)

2.

\(g'\left(x\right)=2x.f'\left(\sqrt{x^2+4}\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\f'\left(\sqrt{x^2+4}\right)=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\\sqrt{x^2+4}=1\\\sqrt{x^2+4}=-2\end{matrix}\right.\)

2 pt cuối đều vô nghiệm nên \(g'\left(x\right)=0\) có đúng 1 nghiệm

Đúng(3)

PT

Pham Trong Bach

19 tháng 8 2018

Tìm a để hàm số f ( x ) = 5 a x 2 + 3 x + 2 a + 1 k h i x ≥ 0 1 + x + x 2 + x + 2 k h i x < 0 có giới hạn tại x → 0 A. +∞ B. -∞ ...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

19 tháng 8 2018

Chọn C.

Ta có:

Vậy

Đúng(0)

PT

Pham Trong Bach

9 tháng 4 2019

Cho hàm số có đồ thị (H). Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 và tiếp xúc với (H) thì phương trình của Δ là A. y = x + 4. D. Không tồn...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

9 tháng 4 2019

Chọn C.

Đạo hàm: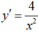

Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 nên có hệ số góc bằng 1.

Ta có phương trình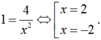

Tại M(2; 0). Phương trình tiếp tuyến là y = x – 2.

Tại N(-2; 4). Phương trình tiếp tuyến là y = x + 6.

Đúng(0)

PL

Phương Lee

4 tháng 4 2021

1. Cho f(x) và g(x) có đạo hàm trên R. Tính đạo hàm của

a, y=f(x³)-g(x²)

b, y=\(\sqrt{f^3\left(x\right)+g^3\left(x\right)}\)

2. Cho f(x)=\(\dfrac{m-1}{4}\)x⁴+ \(\dfrac{m-2}{3}\)x³-mx²+3x-1. Giải và biện luận pt: f'(x)=0

#Toán lớp 11

1

NV

Nguyễn Việt Lâm

Giáo viên

4 tháng 4 2021

1a.

\(y'=3x^2.f'\left(x^3\right)-2x.g'\left(x^2\right)\)

b.

\(y'=\dfrac{3f^2\left(x\right).f'\left(x\right)+3g^2\left(x\right).g'\left(x\right)}{2\sqrt{f^3\left(x\right)+g^3\left(x\right)}}\)

2.

\(f'\left(x\right)=\left(m-1\right)x^3+\left(m-2\right)x^2-2mx+3=0\)

Để ý rằng tổng hệ số của vế trái bằng 1 nên pt luôn có nghiệm \(x=1\), sử dụng lược đồ Hooc-ne ta phân tích được:

\(\Leftrightarrow\left(x-1\right)\left[\left(m-1\right)x^2+\left(2m-3\right)x-3\right]=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(m-1\right)x^2+\left(2m-3\right)x-3=0\left(1\right)\end{matrix}\right.\)

Xét (1), với \(m=1\Rightarrow x=-3\)

- Với \(m\ne1\Rightarrow\Delta=\left(2m-3\right)^2+12\left(m-1\right)=4m^2-3\)

Nếu \(\left|m\right|< \dfrac{\sqrt{3}}{2}\Rightarrow\) (1) vô nghiệm \(\Rightarrow f'\left(x\right)=0\) có đúng 1 nghiệm

Nếu \(\left|m\right|>\dfrac{\sqrt{3}}{2}\Rightarrow\left(1\right)\) có 2 nghiệm \(\Rightarrow f'\left(x\right)=0\) có 3 nghiệm

Đúng(1)

B

Buddy

17 tháng 8 2023

Cho hàm số \(f\left( x \right) = {x^2}{e^x}.\) Tính \(f''\left( 0 \right).\)

#Toán lớp 11

1

H

HaNa

17 tháng 8 2023

`f'(x) = (x^2)'e^x + x^2.(e^x)'`
`= 2xe^x + x^2.e^x`
`= (2x + x^2).e^x`

Tính đạo hàm lần 2 của f(x):
`f''(x) = ((2x + x^2).e^x)'`
`= (2x + x^2)'.e^x + (2x + x^2).(e^x)'`
`= (2 + 2x).e^x + (2x + x^2).e^x`
`= (2 + 4x + x^2).e^x`

Ta thay x = 0 vào công thức trên:
`f''(0) = (2 + 4.0 + 0^2).e^0`
`= 2.1`
`= 2`

Vậy, f''(0) = 2.

Đúng(2)

NK

Nguyễn Kiều Anh

20 tháng 3 2021

Câu 1:Cho f(x)= \(\dfrac{\sqrt{x+2}-\sqrt{2-x}}{x}\), x≠0. Phải bổ sung thêm giá trị f(0) bằng bao nhiêu thì hàm số f(x) liên tục tại x=0?Câu 2:Xét tính liên tục của hàm sốa, f(x)= \(\left\{{}\begin{matrix}x+\dfrac{3}{2}\\\dfrac{\sqrt{x+1}-1}{\sqrt[3]{1+x}-1}\end{matrix}\right.\)khi x≤0 và x>0 tại xo=0b, f(x)= \(\left\{{}\begin{matrix}\dfrac{x^3-x^2+2x-2}{x-1}\\3x+a\end{matrix}\right.\)với x<1 và với x≥1,...

Đọc tiếp

#Toán lớp 11

2

NV

Nguyễn Việt Lâm

Giáo viên

20 tháng 3 2021

1.

\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x+2}-\sqrt{2-x}}{x}=\lim\limits_{x\rightarrow0}\dfrac{2x}{x\left(\sqrt{x+2}+\sqrt{2-x}\right)}=\lim\limits_{x\rightarrow0}\dfrac{2}{\sqrt{x+2}+\sqrt{2-x}}=\dfrac{2}{2\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)

Vậy cần bổ sung \(f\left(0\right)=\dfrac{\sqrt{2}}{2}\) để hàm liên tục tại \(x=0\)

2.

a. \(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(x+\dfrac{3}{2}\right)=\dfrac{3}{2}\)

\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt{x+1}-1}{\sqrt[3]{1+x}-1}=\lim\limits_{x\rightarrow0^+}\dfrac{x\left(\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1\right)}{x\left(\sqrt[]{x+1}+1\right)}\)

\(=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1}{\sqrt[]{x+1}+1}=\dfrac{3}{2}\)

\(\Rightarrow f\left(0\right)=\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)\) nên hàm liên tục tại \(x=0\)

Đúng(1)

NV

Nguyễn Việt Lâm

Giáo viên

20 tháng 3 2021

2b.

\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\dfrac{x^3-x^2+2x-2}{x-1}=\lim\limits_{x\rightarrow1^-}\dfrac{x^2\left(x-1\right)+2\left(x-1\right)}{x-1}\)

\(=\lim\limits_{x\rightarrow1^-}\dfrac{\left(x^2+2\right)\left(x-1\right)}{x-1}=\lim\limits_{x\rightarrow1^-}\left(x^2+2\right)=3\)

\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=f\left(1\right)=\lim\limits_{x\rightarrow1^+}\left(3x+a\right)=a+3\)

- Nếu \(a=0\Rightarrow f\left(1\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^+}f\left(x\right)\) hàm liên tục tại \(x=1\)

- Nếu \(a\ne0\Rightarrow\lim\limits_{x\rightarrow1^-}f\left(x\right)\ne\lim\limits_{x\rightarrow1^+}f\left(x\right)\Rightarrow\) hàm không liên tục tại \(x=1\)

Đúng(1)

B

Buddy

17 tháng 8 2023

Cho hàm số \(f(x)\) thoả mãn \(f(1) = 2\) và \(f'(x) = {x^2}f(x)\) với mọi \(x\). Tính \(f''(1)\).

#Toán lớp 11

1