Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a: Thay x=1 và y=1 vào y=ax+5, ta được:
\(a\cdot1+5=1\)
=>a+5=1
=>a=-4
b: a=-4 nên y=-4x+5
| x | -2 | -1 | 0 | 1/2 | -3 |
| y=-4x+5 | 13 | 9 | 5 | 3 | -7 |
Bài 1:
a: \(y=-2\left(x+5\right)-4\)
\(=-2x-10-4\)
=-2x-14
a=-2; b=-14
b: \(y=\dfrac{1+x}{2}\)
=>\(y=\dfrac{1}{2}x+\dfrac{1}{2}\)
=>\(a=\dfrac{1}{2};b=\dfrac{1}{2}\)

a) Vì đồ thị hàm số đi qua điểm \(M\left( {1; - 2} \right)\)nên ta có:
\( - 2 = a.1 - 4 \Leftrightarrow a = - 2 + 4 = 2\)
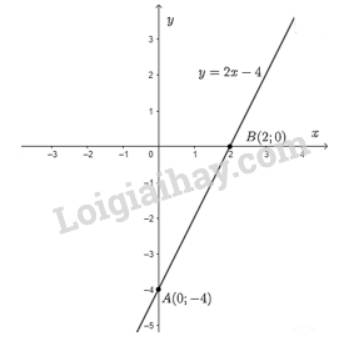
Hàm số cần tìm là \(y = 2x - 4\) có hệ số góc \(a = 2\).
b) Cho \(x = 0 \Rightarrow y = - 4\) ta được điểm \(A\left( {0; - 4} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{4}{2} = 2\) ta được điểm \(B\left( {2;0} \right)\) trên \(Ox\).
Đồ thị hàm số là đường thẳng đi qua hai điểm \(A\) và \(B\).

Để hai đường thẳng \(y = ax + 2\) và \(y = 9x - 9\) song song với nhau thì \(\left\{ \begin{array}{l}a = 9\\2 \ne - 9\end{array} \right. \Rightarrow a = 9\).
Do đó, để đường thẳng \(y = ax + 2\) song song với đường thẳng \(y = 9x - 9\) thì \(a = 9\).

Ta có: \(\left(a^2+b^2\right)\left(x^2+y^2\right)=\left(ax+by\right)^2\)
\(\Leftrightarrow a^2x^2+a^2y^2+b^2x^2+b^2y^2=a^2x^2+b^2y^2+2axby\)
\(\Leftrightarrow a^2y^2-2axby+b^2x^2=0\)
\(\Leftrightarrow\left(ay-bx\right)^2=0\)
\(\Leftrightarrow ay=bx\)
hay \(\dfrac{a}{x}=\dfrac{b}{y}\)
Ta có : \(\left(a^2+b^2\right)\left(x^2+y^2\right)=\left(ax+by\right)^2\)
\(\Leftrightarrow a^2x^2+a^2y^2+b^2x^2+b^2y^2=a^2x^2+2abxy+b^2y^2\)
\(\Leftrightarrow a^2y^2-2abxy+b^2x^2=0\)
\(\Leftrightarrow\left(ay-bx\right)^2=0\)
\(\Leftrightarrow ay-bx=0\)
\(\Leftrightarrow ay=bx\Leftrightarrow\dfrac{a}{b}=\dfrac{x}{y}\)

Áp dụng bđt bunhiacopxki \(\left(a^2+b^2\right)\left(x^2+y^2\right)\ge\left(ax+by\right)^2\)
dấu "=" xảy ra \(< =>ay=bx< =>\frac{a}{x}=\frac{b}{y}\)

Lời giải:
a. Để hs trên là hàm bậc nhất thì:
$4m2-4m+1\neq 0$
$\Leftrightarrow (2m-1)^2\neq 0$
$\Leftrightarrow 2m-1\neq 0$
$\Leftrightarrow m\neq \frac{1}{2}$
b.
$f(1)=(4m^2-4m+1).1-3=4m^2-4m-2=6$
$\Leftrightarrow 4m^2-4m-8=0$
$\Leftrightarrow m^2-m-2=0$
$\Leftrightarrow (m+1)(m-2)=0$
$\Leftrightarrow m=-1$ hoặc $m=2$