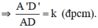Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) BE // DC => ∆BEF ∽ ∆CDF
AD // BF => ∆ADE ∽ ∆BFE.
Do đó: ∆ADE ∽ ∆CFD
b) BE = AB - AE = 12 - 8 = 4cm
∆ADE ∽ ∆BFE => \(\dfrac{AE}{BE}=\dfrac{AD}{BF}=\dfrac{DE}{FD}\)
=> \(\dfrac{8}{4}=\dfrac{7}{BF}=\dfrac{10}{EF}\)
=> BF = 3,5 cm.
EF = 5 cm.
Vì mình chưa đc làm CTV nên kh đăng ảnh lên được , bạn thông cảm :
Bạn vào thống kê hỏi đáp mình là có ảnh nhé
Tham khảo thêm : https://lazi.vn/edu/exercise/406693/chung-minh-rang-neu-tam-giac-abc-dong-dang-voi-tam-giac-abc-theo-ti-so-k-thi-ti-so-cua-hai-duong-trung-tuyen-tuong-ung-cua-hai-tam
https://lazi.vn/edu/exercise/406693/chung-minh-rang-neu-tam-giac-abc-dong-dang-voi-tam-giac-abc-theo-ti-so-k-thi-ti-so-cua-hai-duong-trung-tuyen-tuong-ung-cua-hai-tam
Tham Khảo link trên nha bn
a) Xét tam giác BKC và CHB có:
góc B= góc C (tính chất tam giác cân)
góc BKC = góc BHC = 90 độ
=> Tam giác BKC đồng dạng tam giác CHB
=> \(\frac{BK}{CH}=\frac{BC}{BC}=1=k\)
b) Tam giác BHA đồng dạng tam giác CKA (g-g)
=> \(\frac{HA}{AK}=\frac{BA}{AC}=1\)
=> \(\frac{AK}{AB}=\frac{AH}{AC}\)
=> KH//BC (Định lí Ta - lét đảo)
c) Ta có theo hệ quả Ta-let:
\(\frac{AK}{AB}=\frac{KH}{BC}=>\frac{AK}{b}=\frac{KH}{a}=>KH=\frac{a.AK}{b}\)
Ta có: AK2+KC2=b2 (1)
KC2+KB2=a2 => KC2+(b-AK)2=a2 =>KC2-2b.AK+AK2=a2 (2)
Trừ 2 cho 1, ta có: -2b.AK=a2-b2 =>\(AK=\frac{a^2-b^2}{-2b}\)
Từ đó => \(KH=\frac{a\times\frac{a^2-b^2}{-2b}}{b}\)
Giả sử ΔA’B’C’ 
ΔABC theo tỉ số k
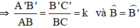
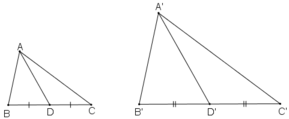
Gọi D, D’ lần lượt là trung điểm BC và B’C’
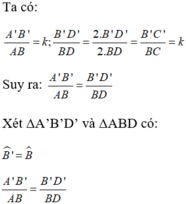
⇒ ΔA’B’D’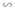 
ΔABD theo tỉ số k.
Gọi AD và A’D' lần lượt là hai đường phân giác của ΔABC và ΔA'B'C'.
+) Lại có; AD, A’D’ lần lượt là phân giác của góc A và góc A’ nên:
Gọi AD và A’D' lần lượt là hai đường phân giác của ΔABC và ΔA'B'C'.
+) Lại có; AD, A’D’ lần lượt là phân giác của góc A và góc A’ nên:
