
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

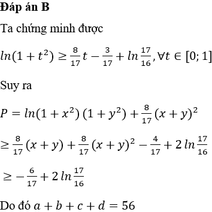

áp án B
Ta có: log 3 x + 1 y + 1 y + 1 = 9 − x − 1 y + 1 ⇔ y + 1 log 3 x + 1 y + 1 + x − 1 y + 1 = 9
⇔ y + 1 log 3 c + 1 y + 1 + x + 1 y + 1 − 2 y = 11
⇔ y + 1 log 3 c + 1 y + 1 − 2 = 9 − x + 1 y + 1 *
Nếu x + 1 y + 1 > 9 ⇒ V T * > 0 ; V P * < 0
Ngược lại nếu x + 1 y + 1 < 9 ⇒ V T * < 0 ; V P * > 0
Do đó * ⇔ x + 1 y + 1 = 9 ⇔ x y + x + y = 8
Khi đó P = x + y 3 − 3 x y x + y − 57 x + y = x + y 3 − 3 8 − x − y x + y − 57 x + y
Đặt t = x + y ≥ 2 ⇒ f t = t 3 − 3 8 − t t − 57 t = t 3 + 3 t 2 − 81 t
⇒ f ' t = 3 t 2 + 6 t − 81 = 0 ⇒ t = − 1 + 2 7 ⇒ P min = f − 1 + 2 7 = 83 − 112 7 ⇒ a + b = − 29

Đáp án A
Ta có: x = 1 ⇒ y = - 2 ⇒ - 2 = 1 + b a - 2 ⇔ - 2 a + 4 = b + 1 ⇔ 2 a + b = 3
Do tiếp tuyến A song song với đường thẳng d : 3 x + y - 4 = 0 hay y = - 3 x + 4 nên y ' 1 = - 2 - a b a - 2 2 = - 3 ⇒ - 2 - a 3 - 2 a a - 2 2 = - 3 ⇔ - 2 a 2 + 3 a + 2 a - 2 2 = - 3 ⇔ a - 2 - 2 a - 1 a - 2 2 = - 3
⇔ - 2 a - 1 = - 3 ⇔ a = 1 ⇒ b = 1 ⇒ a - 3 b = - 2

Đáp án B.
Từ
f x . f ' x = 2 x f 2 x + 1 ⇒ f x . f ' x f 2 x + 1 = 2 x ⇒ ∫ f x . f ' x f 2 x + 1 d x = ∫ 2 x d x
(1)
Đặt
f 2 x + 1 = t ⇒ f 2 x = t 2 − 1 ⇒ 2 f x . f ' x d x = 2 t d t ⇒ f x . f ' x d x = t d t
Suy ra ∫ f x . f ' x f 2 x + 1 x = ∫ t d t t = ∫ d t = t + C 1 = f 2 x + 1 + C 1 và ∫ 2 x d x = x 2 + C 2
Từ (1) ta suy ra f 2 x + 1 + C 1 = x 2 + C 2 . Do f 0 = 0 nên C 2 − C 1 = 1 .
Như vậy
f 2 x + 1 = x 2 + C 2 − C 1 = x 2 + 1 ⇒ f 2 x = x 2 + 1 2 − 1 = x 4 + 2 x 2
⇒ f x = x 4 + 2 x 2 = x x 2 + 2 = x x 2 + 2
(do x ∈ 1 ; 3 ).
Ta có f ' x = x 2 + 2 + x 2 x 2 + 2 = 2 x 2 + 1 x 2 + 2 > 0, ∀ x ∈ ℝ ⇒ Hàm số f x = x x 2 + 2 đồng biến trên R nên f x cũng đồng biến trên 1 ; 3 .
Khi đó M = max 1 ; 3 f x = f 3 = 3 11 và m = min 1 ; 3 f x = f 1 = 3 .
Vậy
P = 2 M − m = 6 11 − 3 ⇒ a = 6 ; b = 1 ; c = 0 ⇒ a + b + c = 7