Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

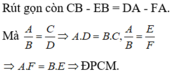


Xét \(\Delta D'E'F':\)
\(\widehat{D'}+\widehat{E'}+\widehat{F'}=180^o\) (Tổng 3 góc trong tam giác).
\(\Rightarrow\widehat{D'}+60^o+50^o=180^o.\\ \Rightarrow\widehat{D'}=70^o.\\ \Rightarrow\widehat{D'}=\widehat{A'}\left(=70^o\right).\)
Xét \(\Delta A'B'C'\) và \(\Delta D'E'F':\)
\(\widehat{A'}=\widehat{D'}\left(cmt\right).\)
\(\widehat{B'}=\widehat{E'}\left(=60^o\right).\)
\(\Rightarrow\) \(\Delta A'B'C'\sim\) \(\Delta D'E'F'\left(g-g\right).\)
\(\Rightarrow\dfrac{B'C'}{E'F'}=\dfrac{A'C'}{D'F'}\) (2 cạnh tương ứng).
\(\Rightarrow B'C'.D'F'=A'C'.E'F'.\)

a: \(\widehat{C'}=180^0-60^0-70^0=50^0\)
Xét ΔA'B'C' và ΔD'E'F' có
\(\widehat{B'}=\widehat{E'};\widehat{C'}=\widehat{F'}\)
Do đó:ΔA'B'C'\(\sim\)ΔD'E'F'
b: Ta có: ΔA'B'C'\(\sim\)ΔD'E'F'
nên A'C'/D'F'=B'C'/E'F'
hay \(A'C'\cdot E'F'=B'C'\cdot D'F'\)

a) Gọi P và Q lần lượt là giao điểm của AE, AF với CD.
Chứng minh tương tự 2B.
b) Ta có:
M N = 1 2 ( A B + C D ) = 1 2 ( a + c )
Lại có:
c = CD = CQ + QD = BC + QD = b + QD (do tam giác BCQ cân) Þ QD = c - b.
Trong hình thang ABQD có M là trung điểm của AD và MF//DQ nên chứng minh được F là trung điểm của BQ, từ đó chứng minh MF là đường trung bình của hình thang ABQD.
Vì MF là đường trung bình của hình thang ABQD.
Þ M F = 1 2 ( A B + D Q ) = 1 2 ( a + c − b )
Mặt khác, FN là đường trung bình của tam giác BCQ, tức là F N = 1 2 C Q = 1 2 b .