Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

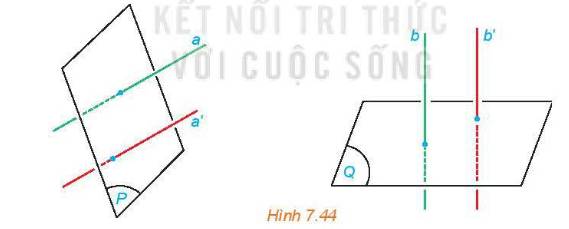
Vì hai đường thẳng a, a' cùng vuông góc với (P), hai đường thẳng b, b' cùng vuông góc với (Q) nên a // a', b // b'
Vậy (a,b) = (a', b')

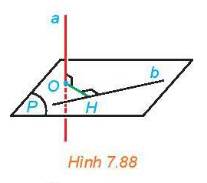
\(a\perp\left(P\right)\) tại O
\(OH\subset\left(P\right)\)
Do đó: \(a\perp OH\)
mà \(b\perp OH\)
nên \(d\left(a;b\right)=OH\)

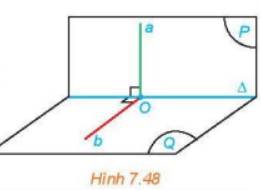
a) \(\left. \begin{array}{l}\left( P \right) \cap \left( Q \right) = \Delta \\\left( P \right):a \bot \Delta \\\left( Q \right):b \bot \Delta \end{array} \right\} \Rightarrow \left( {\left( P \right),\left( Q \right)} \right) = \left( {a,b} \right)\)
Mà \(\left( P \right) \bot \left( Q \right) \Rightarrow \left( {\left( P \right),\left( Q \right)} \right) = {90^0} \Rightarrow \left( {a,b} \right) = {90^0}\)
b) \(\left( {a,b} \right) = {90^0} \Rightarrow a \bot b,a \bot \Delta ,b \cap \Delta \Rightarrow a \bot \left( Q \right)\)

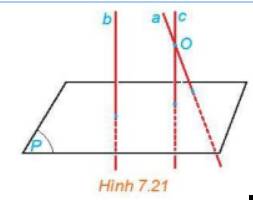
a) b // c; b ⊥ (P) ⇒ c ⊥ (P)
Mà a ⊥ (P)
a, c cùng đi qua điểm O
⇒ a trùng c.
b) Ta có b // c mà a trùng c nên a // b.

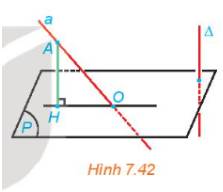
+) AH // \(\Delta \) (cùng vuông góc (P))
\( \Rightarrow \) (a, \(\Delta \)) = (a, AH) = \(\widehat {HAO}\)
+) HO là hình chiếu của a trên (P)
\( \Rightarrow \) (a, (P)) = (a, HO) = \(\widehat {AOH}\)
Mà tam giác AHO vuông tại H \( \Rightarrow \) \(\widehat {HAO}\) và \(\widehat {AOH}\) phụ nhau.
\( \Rightarrow \) Góc giữa a và (P) có mối quan hệ với góc giữa a và \(\Delta \) là 2 góc phụ nhau.

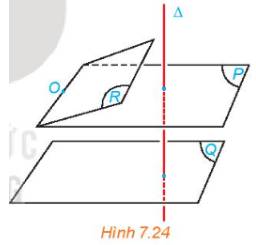
a) (R) // (Q); \(\Delta \) \( \bot \) (Q) \( \Rightarrow \) \(\Delta \) \( \bot \) (R)
Mà \(\Delta \) \( \bot \) (P) và (R), (Q) là 2 mặt phẳng cùng đi qua O
\( \Rightarrow \) (R) trùng (P)
b) (R) // (Q) mà (R) trùng (P) nên (P) // (Q)

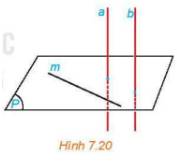
\(\left. \begin{array}{l}a \bot \left( P \right)\\m \subset \left( P \right)\end{array} \right\} \Rightarrow a \bot m \Rightarrow \left( {a,m} \right) = {90^0}\)
a // b \( \Rightarrow \left( {a,m} \right) = \left( {b,m} \right) = {90^0}\) mà đường thẳng m bất kì thuộc mặt phẳng (P)
\( \Rightarrow \) b \( \bot \) (P).

a) Vì (P) // (Q), (R) cắt (P) suy ra (R) cũng cắt (Q).
b) a và b lần lượt là giao tuyến của (R) và các mp(P), (Q) do đó a và b đồng phẳng suy ra a và b không thể chéo nhau.
Mà a và b lần lượt thuộc hai mặt phẳng song song (P) và (Q) suy ra a // b.
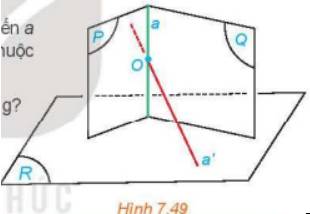

a) Vì O là một điểm thuộc a là giao tuyến của hai mặt phẳng (P), (Q) và a' là đường thẳng qua O và vuông góc với (R).
Theo nhận xét trang 46 thì a' có nằm trong các mặt phẳng (P), (Q).
b) Vì a' có nằm trong các mặt phẳng (P), (Q) nên a’ là giao tuyến của hai mặt phẳng (P), (Q) do đó a trùng a' (do a cũng là giao tuyến của hai mặt phẳng (P), (Q)).
c) a vuông góc với (R) do a trùng a’ và a’ vuông góc với (R).