Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhận thấy tứ giác MFNE có góc M và N vuông --> góc MFN+góc MEN= 2 vuông (*)
Lại có các tam giác AFB và MEN đồng dạng (vì có góc NME=gocFAB và góc MNE =góc FBA), suy ra góc AFB=góc MEN --> góc MFN=góc MEN (**), từ (*); (**) suy ra góc MFN=góc MEN =1 vuông
--> tứ giác MENF là hình chữ nhật, từ đó dễ dàng suy ra tiếp FE vuông góc với AB
b) Gọi I ; K lần lượt là trung điểm của O1O2 và MN. Áp dụng Talét dễ dàng tính được IK=5
--> KD^2=ID^2-IK^2 =9^2 -5^2 =56 --> CD=2.KD= 4√14

a. b.
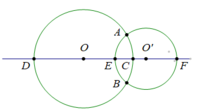
c. - Đường tròn (O’; 1cm) có đường kính là: EF; Các dây cung là: EA, EB, AB, FA, FB
Vì E thuộc (O’; 1cm) nên EO’=1cm; EF=2.EO’=2cm
- Đường tròn (O; 1,5cm) có đường kính là: DC; Các dây cung là: DA, DB, AB, AC, CB
Vì C thuộc (O; 1,5cm) nên CO=1,5cm; DC=2.CO=3cm
d. Vì đường tròn (O’; 1cm) cắt đoạn thẳng OO’ tại E, nên E nằm giữa 2 điểm O và O’.
Ta có: O E + E O ' = O O ' ⇒ O E = 1 c m
Mà EO’=1cm, nên OE=EO’ (=1cm)
Do đó: E là trung điểm của đợn thẳng OO’.
e. Vì đường tròn (O; 1cm) cắt đường thẳng OO’ tại D, đường tròn (O’; 1cm) cắt đường thẳng OO’ tại F, nên 4 điểm D, O, O’, F lần lượt theo thứ tự đó và DO=1,5cm; O’F=1cm.
Ta có: D F = D O + O O ' + O ' F = 1 , 5 + 2 + 1 = 4 , 5 c m .
Vậy DF=4,5cm

Bài 3:
a: Xét ΔABM và ΔACN có
AB=AC
góc ABM=góc ACN
BM=CN
Do đó: ΔABM=ΔACN
Suy ra: AM=AN
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH=góc CAK
Do đó; ΔAHB=ΔAKC
Suy ra: AH=AK và BH=CK
c: Xét ΔHBM vuông tại H và ΔKCN vuông tại K có
MB=CN
góc M=góc N
Do đó ΔHBM=ΔKCN
Suy ra: góc HBM=góc KCN
=>góc OBC=góc OCB
hay ΔOBC can tại O

Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
=> BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE.
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
=>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
(Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/
(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
=> ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).
Em tham gia
em lên sp vs
@!Nhất
"Một mà hai nhưng hai là một" ( ͡° ͜ʖ ͡°)
Cho me tham gia ❤‿❤