Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Gắn hệ trục tọa độ Oxy sao cho O 1 ≡ O (gốc tọa độ).
Phương trình đường tròn O 1 ; 5 là x 2 + y 2 = 5 2 ⇒ y = ± 25 − x 2 .
Tam giác O 1 O 2 A vuông tại O 2 , có O 1 O 2 = O 1 A 2 − O 2 A 2 = 5 2 − 3 2 = 4.
Phương trình đường tròn O 2 ; 3 là x − 4 2 + y 2 = 9 ⇒ y = ± 9 − x − 4 2 .
Gọi V 1 là thể tích của khối tròn xoay sinh ra khi quay hình phẳng D 1 được giới hạn bởi các đường y = 9 − x − 4 2 , y = 0 , x = 4 , x = 7 quanh trục tung ⇒ V 1 = π ∫ 4 7 9 − x − 4 2 d x .
Gọi V 2 là thể tích của khối tròn xoay sinh ra khi quay hình phẳng D 2 được giới hạn bởi các đường y = 25 − x 2 , y = 0 , x = 4 , x = 5 quanh trục tung ⇒ V 2 = π ∫ 4 5 25 − x 2 d x .
Khi đó, thể tích cần tính là:
V = V 1 − V 2 = π ∫ 4 7 9 − x − 4 2 d x − π ∫ 4 5 25 − x 2 d x = 40 π 3 .

Đáp án B
Ta có V = π ∫ 0 π − sin x 2 d x = π ∫ 0 π sin 2 x d x

Giải phương trình:
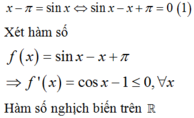
Phương trình (1) có tối đa 1 nghiệm. Mà f π = 0 ⇒ x = π là nghiệm duy nhất của (1).
Thể tích khối tròn xoay tạo thành là:
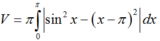
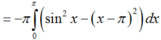
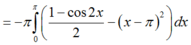

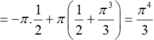
Mà
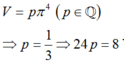
Chọn A.

Đáp án D
Thể tích khối tròn xoay cần tính là
V = π ∫ 0 π sin 2 2 x d x = π ∫ 0 π 1 − cos 4 x 2 d x = π 2 x − 1 4 sin 4 x 0 π = π 2 π − 0 = π 2 2 .

Đáp án B.
Phương pháp: Ứng dụng tích phân để tính thể tích khối tròn xoay.
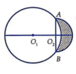
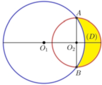
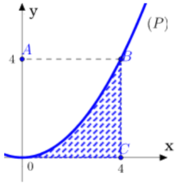
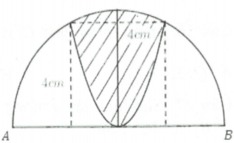
Cách giải: Gắn hệ trục tọa độ Oxy như hình vẽ:
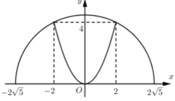
Ta có:
Phương trình đường tròn: ![]()
Phương trình parabol: ![]()
Thể tích khối cầu 
Thể tích khi quay phần tô đậm quanh trục Ox là: 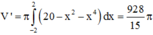
=> Thể tích cần tính 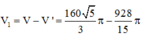
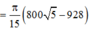





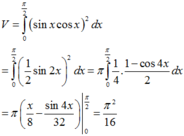

Đáp án C
Chọn hệ tọa độ Oxy như hình vẽ với O 3 ≡ O , O 2 C ≡ O x , O 2 A ≡ O y .
Ta có
O 1 O 2 = O 1 A 2 − O 2 A 2 = 5 2 − 3 2 = 4 ⇒ O 1 − 4 ; 0 .
Phương trình đường tròn O 1 : x + 4 2 + y 2 = 25.
Phương trình đường tròn O 2 : x 2 + y 2 = 9.
Kí hiệu H 1 là hình phẳng giới hạn bởi các đường O 2 : x 2 + y 2 = 9, trục Oy: x = 0 khi x ≥ 0 .
Kí hiệu H 2 là hình phẳng giới hạn bởi các đường O 2 : x 2 + y 2 = 9, trục Oy: x=0 khi x ≥ 0 .
Khi đó thể tích V cần tìm chíình bằng thể tích V 2 của khối tròn xoay thu được khi quay hình H 2 xung quanh trục Ox (thể tích nửa khối cầu bán kính bằng 3) trừ đi thể tích V 1 của khối tròn xoay thu được khi quay hình H 1 xung quanh trục Ox.
Ta có V 2 = 1 2 . 4 3 π 3 3 = 18 π (đvtt);
V 1 = π ∫ 0 1 y 2 d x = π ∫ 0 1 25 − x + 4 2 d x = 14 π 3 (đvtt).
Vậy V = V 2 − V 1 = 18 π − 14 π 3 = 40 π 3 (đvtt).