Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABC và ΔABD, ta có:
AC = AD (bằng bán kính đường tròn (A))
Ab cạnh chung
BC = BD (bằng bán kính đường tròn (B))
Suy ra: ΔABC = ΔABD (c.c.c)
Xét ΔABC và ΔABD, ta có:
AC = AD (bằng bán kính đường tròn (A))
Ab cạnh chung
BC = BD (bằng bán kính đường tròn (B))
Suy ra: ΔABC = ΔABD (c.c.c)

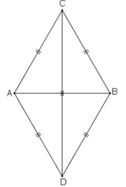
Xét ΔABC và ΔABD, ta có:
AC = AD (bằng bán kính đường tròn (A))
Ab cạnh chung
BC = BD (bằng bán kính đường tròn (B))
Suy ra: ΔABC = ΔABD (c.c.c)

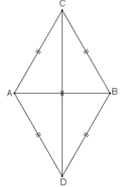
Xét ΔACD và ΔBCD, ta có:
AC = BC (= AB)
CD cạnh chung
AD = BD (= AB)
Suy ra: ΔACD = ΔBCD(c.c.c)

Tham khảo
ΔΔABC và ΔΔDCB có AB=CD (gt)
BC chung AC=DB (gt)
Vậy ΔΔABC = ΔΔDCB (c.c.c)
Suy ra ˆBDC=ˆA=800BDC^=A^=800 (hai góc tương ứng)
b) Do ΔΔABC = ΔΔDCB (câu a) do đó ˆABC=ˆBCDABC^=BCD^ (hai góc tương ứng của hai tam giác bằng nhau)
Hai góc này ở vị trí so le trong của hai đường thẳng AB và CD cắt đường thẳng BC do đó CD // AB.

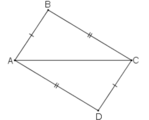
Xét ΔABC và ΔCDA, ta có:
AB = CD (theo cách vẽ)
AC cạnh chung
BC = AD (theo cách vẽ)
Suy ra: ΔABC = ΔCDA (c.c.c) ⇒ ∠(ACB) =∠(CAD) (hai góc tương ứng)
Vậy AD // BC ( vì có cặp góc so le trong bằng nhau)


a) Xét tam giác NMA và NMB có:
\(MA=MB\left(gt\right)\)
\(NM\) là cạnh chung.
\(NA=NB\) (đường tròn tâm A và B cùng bán kính cắt nhau)
\(\Rightarrow\Delta NMA=\Delta NMB\left(c.c.c\right)\) (1)
b) Vì \(\widehat{NMA}=\widehat{NMB}\) (từ 1) và 2 góc trên là 2 góc kề bù nên \(\widehat{NMA}=\widehat{NMB}=90^o\)
Vậy \(NM\perp AB\)
c) \(NA=NB\) (từ 1)
\(BM=\dfrac{AB}{2}=\dfrac{12}{2}=6\left(cm\right)\)
Chu vi tam giác NMB:
\(10+8+6=24\left(cm\right)\)
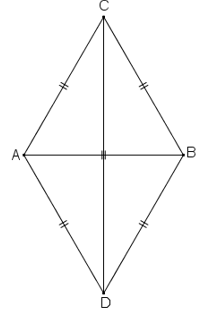
a: Xét ΔABE và ΔABF có
BE=BF
AB chung
AE=AF
Do đó: ΔABE=ΔABF
b: Xét ΔAEF và ΔBEF có
AE=BE
EF chung
AF=BF
Do đó: ΔAEF=ΔBEF
c: Xét tứ giác AEBF có
AE=BF
BE=AF
Do đó: AEBF là hình bình hành
=>AE//BF; AF//BE