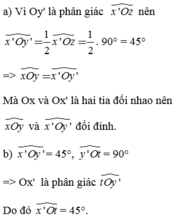Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

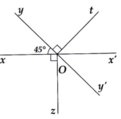
Theo đề ta có:
\(\widehat{tOx}+\widehat{t'Oy'}+\widehat{xOy'}=\dfrac{1}{2}\widehat{xOy}+\dfrac{1}{2}\widehat{x'Oy'}+\widehat{xOy'}\)
Mà \(\widehat{xOy}=\widehat{x'Oy'}\) (hai góc đối đỉnh)
Suy ra biểu thức trên bằng \(\widehat{xOy}+\widehat{xOy'}=180^o\) (hai góc kề bù)
Hay \(\widehat{tOx}+\widehat{t'Oy'}+\widehat{xOy'}=\widehat{tOt'}=180^o\)
Từ đó suy ra tt' là một góc bẹt, hay tia Ot và tia Ot' là hai tia đối nhau

Ta có: \(\widehat{xOz}=\dfrac{\widehat{xOy}}{2}=\dfrac{30^0}{2}=15^0\)
\(\Leftrightarrow\widehat{zOx'}=180^0-15^0=165^0\)

Ta có: Oz là tia phân giác của \(\widehat{xOy}\) (gt)
\(\Rightarrow\widehat{xOz}=\widehat{yOz}\)
Vì \(Oz\perp Oz'\) (gt) nên: \(\widehat{yOz}+\widehat{yOz'}=90^o\)
Lại có: \(\widehat{xOz}+\widehat{yOz}+\widehat{yOz'}+\widehat{x'Oz'}=180^o\)
\(\Rightarrow\widehat{xOz}+\widehat{x'Oz'}=180^o-\left(\widehat{yOz}+\widehat{yOz'}\right)\)
\(=180^o-90^o=90^o\)
\(\Rightarrow\widehat{xOz}+\widehat{x'Oz'}=\widehat{yOz}+\widehat{yOz'}=90^o\)
Mà \(\widehat{xOz}=\widehat{yOz}\) (cmt)
\(\Rightarrow\widehat{x'Oz'}=\widehat{yOz'}\)
`=>` Tia Oz' là tia phân giác của \(\widehat{x'Oy}\) (đpcm)