Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét : \(\widehat{BOC}+\widehat{DOC}=\widehat{DOB}\)
\(\widehat{AOD}+\widehat{DOC}=\widehat{AOC}\)
Mà \(\widehat{DOC}=\widehat{AOC}\)
Vì góc DOB và góc AOC là hai góc vuông nên
\(\widehat{AOD}=\widehat{BOC}=90^0\)
Ta có: góc AOC= góc BOD (=90độ) <=> góc AOD +góc DOC = góc DOC + góc COB <=> góc AOD = góc BOC
OM là phân giác của góc COD => góc DOM = góc COM
=> góc AOD + góc DOM = góc BOC + góc COM <=> góc AOM = góc BOM
Và vì OM là phân giác COD nên OM nằm giữa OA và OB
=> OM là phân giác góc AOB

Mãi trong cô đơn trong CHTT có đó tick mk nha

a, Ta có
\(\widehat{AOD}=\widehat{AOB}-\widehat{BOD}\)
\(\Rightarrow\widehat{AOD}=130^0-90^0=40^0\) [ 1 ]
Mặt khác
\(\widehat{BOC}=\widehat{AOB}-\widehat{AOC}\)
\(\Rightarrow\widehat{BOC}=130^0-90^0=40^0\) [ 2 ]
Từ [ 1 ] và [ 2 ] suy ra
\(\widehat{AOD}=\widehat{BOC}=40^0\)
b.Ta thấy
\(\widehat{AOB}=\widehat{AOD}+\widehat{COD}+\widehat{BOC}\)
\(\Rightarrow\widehat{COD}=\widehat{AOB}-2\widehat{AOD}\)[ vì góc AOD = góc BOC theo câu a ]
\(\Rightarrow\widehat{COD}=130^0-2.40^0\)
\(\Rightarrow\widehat{COD}=130^0-80^0=50^0\)
Vậy góc COD = 50độ
c.Vì OM là tia phân giác góc COD nên
\(\widehat{COM}=\widehat{DOM}=\frac{\widehat{COD}}{2}=\frac{50^0}{2}=25^0\)
Ta có
\(\widehat{AOM}=\widehat{AOD}+\widehat{DOM}\)
\(\Rightarrow\widehat{AOM}=40^0+25^0=65^0\)
mà \(\widehat{BOM}=\widehat{BOC}+\widehat{COM}\)
\(\Rightarrow\widehat{BOM}=40^0+25^0=65^0\)
Suy ra \(\widehat{AOM}=\widehat{BOM}\)
Vậy OM là tia phân giác góc AOB
Chúc bạn học tốt

a) OC và OD lần lượt vuông góc với OA và OB
⇒Góc AOC=Góc BOD=90o⇒Góc AOC=Góc BOD=90o
Ta có:
Góc AOC=AOD+DOC
Góc BOD=BOC+DOC
⇒AOD=BOC


a. Ta có:
O A ⊥ O C ( G T ) ⇒ A O C ^ = 90 ° O D ⊥ O B ( G T ) ⇒ D O B ^ = 90 ° A O D ^ + C O D ^ = A O C ^ = 90 ° B O C ^ + C O D ^ = D O B ^ = 90 °
⇒ A O D ^ = B O C ^ (Cùng phụ C O D ^ )
b. Ta có:
A O D ^ + B O D ^ = A O B ^ ⇒ A O D ^ + 90 ° = 130 ° ⇒ A O D ^ = 130 ° − 90 ° ⇒ A O D ^ = 40 °
Mà A O D ^ + C O D ^ = 90 ° ( C M T )
40 ° + C O D ^ = 90 ° C O D ^ = 50 °
c. OM là tia phân giác của A O B ^ nên:
A O M ^ = B O M ^ = A O B ^ 2 = 65 °
A O D ^ + D O M ^ = A O M ^ 40 ° + D O M ^ = 65 ° D O M ^ = 25 °
Tương tự ta tìm được C O M ^ = 25 °
Do đó C O M ^ = D O M ^ ( = 25 ° )
Vậy OM là tia phân giác của C O D ^
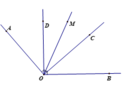

a) Ta có AOC = BOD (= 90o)
=> AOC - COD = BOD - COD
=> AOD = BOC
b) Ta có AOC + BOC = AOB
90o + BOC = 130o
BOC = 40o
Ta có COD + BOC = DOB
COD + 40o = 90o
COD = 50o
c) Ta có OM là tia phân giác của COD
=> DOM = MOC
=> DOM + AOD = MOC + COB (AOD = COB)
=> AOM = MOB
Mà OM nằm giữa hai tia OA và OB
=> OM là tia phân giác của AOB
Tương tự cho trường hợp ngược lại
a) Ta có : \(OC\perp OA\Rightarrow\widehat{AOC}=90^O\)
\(OD\perp OB\Rightarrow\widehat{BOD}=90^O\)
Các tia OC , OD nằm trong \(\widehat{AOB}\)nên :
\(\widehat{AOD}\)\(=\widehat{AOB}\)\(-\widehat{BOD}\)\(=\widehat{AOB}\)\(-90^O\)
\(\widehat{BOC}=\widehat{AOB}-\widehat{AOC}=\widehat{AOB}-90^O\)
\(\Rightarrow\widehat{AOB}=\widehat{BOC}\)
b) Vì \(\widehat{AOC}< \widehat{AOB}\)( góc vuông nhỏ hơn góc tù )
=> OC nằm giữa hai tia OA và OB.
Vì \(\widehat{BOD}< \widehat{AOB}\)( góc vuông nhỏ hơn góc tù )
=> OD nằm giữa hai tia OA và OB
=> OC và OD nằm giữa hai tia OA và OB
=> Phân giác OM của \(\widehat{COD}\)nằm giữa hai tia OA và OB. ( 1)
Lại có : \(\widehat{MOC}=\widehat{MOD}\)
Theo chứng minh trên ta có : \(\widehat{BOC}=\widehat{AOD}\Rightarrow\widehat{MOC}+\widehat{BOC}=\widehat{MOD}+\widehat{AOD}hay\widehat{MCB}=\widehat{MOA}\)( 2 )
Từ (1) và (2) => OM là tia phân giác của \(\widehat{AOB}\)
# Aeri #
Ta có: OC⊥OAOC⊥OA nên ˆAOC=900AOC^=900
OD⊥OBOD⊥OB nên ˆBOD=900BOD^=900 các tia OC, OD ở trong góc AOB nên:
ˆAOD=ˆAOB−ˆBOD=ˆAOB−900AOD^=AOB^−BOD^=AOB^−900
ˆBOC=ˆAOB−ˆAOC=ˆAOB−900BOC^=AOB^−AOC^=AOB^−900
⇒ˆAOD=ˆBOC⇒AOD^=BOC^
b.
Vì ˆAOC<ˆAOBAOC^<AOB^ (góc vuông nhỏ hơn góc tù)
⇒OC⇒OC nằm giữa hai tia OA và OB.
ˆBOD<ˆAOBBOD^<AOB^ (góc vuông nhỏ hơn góc tù)
⇒OD⇒OD nằm giữa hai tia OA và OB
⇒OC⇒OC và OD nằm giữa hai tia OA và OD
⇒⇒ Phân giác OM của góc ˆCODCOD^ nằm giữa hai tia OA và OB (*)
Mặt khác: Do OM là phân giác của góc ˆCODCOD^ nên ˆMOC=ˆMODMOC^=MOD^
Theo chứng minh trên, ta có:
ˆBOC=ˆAOD⇒ˆMOC+ˆBOC=ˆMOD+ˆAODBOC^=AOD^⇒MOC^+BOC^=MOD^+AOD^ hay ˆMCB=ˆMOAMCB^=MOA^ (**)
Từ (*) và (**) ⇒OM⇒OM là tia phân giác góc AOB.