Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

góc AOC+góc BOC=180 độ
=>góc BOC=180-150=30 độ
góc AOD+góc BOD=180 độ
=>góc AOD=180-150=30 độ
góc AOD=góc BOE(hai góc đối đỉnh)
góc AOD=góc BOC(=30 độ)
=>góc BOC=góc BOE
=>OB là phân giác của góc COE

a) Ta có : \(\widehat{AOC}+\widehat{COB}=180^o\)( kề bù )
\(135^o+\widehat{COB}=180^o\)
\(\widehat{COB}=180^o-135^o\)
\(\widehat{COB}=45^o\)
Ta có : \(\widehat{BOC}+\widehat{COD}=\widehat{BOD}\)
\(45^o+\widehat{COD}=135^o\)
\(\widehat{COD}=135^o-45^o\)
\(\widehat{COD}=90^o\)
Ta có : \(\widehat{DOC}+\widehat{COE}=180^o\)( kề bù )
\(90^o+\widehat{COE}=180^o\)
\(\widehat{COE}=90^o\)
\(\Rightarrow OC\perp OE\)
b) Ta có : \(\widehat{COB}+\widehat{BOE}=\widehat{COE}\)
\(45^o+\widehat{BOE}=90^o\)
\(\widehat{BOE}=90^o-45^o\)
\(\widehat{BOE}=45^o\)
\(\Rightarrow\widehat{BOE}=\widehat{COB}=\frac{\widehat{COE}}{2}\)
Vậy OB là tia phân giác của \(\widehat{COE}\)
Bài giải
Ta có : \(\widehat{AOC}=\widehat{BOD}\left(=135^o\right)\)
\(\widehat{DOC}\) chung và OC và OD cùng nằm trên cùng một nửa mặt phẳng nên \(\widehat{DOA}=\widehat{COB}\)
Mà \(\widehat{DOA}=\widehat{EOB}\) ( hai góc đối đỉnh ) nên \(\widehat{BOC}=\widehat{BOE}\)
\(\Rightarrow\text{ }OB\text{ là tia phân giác }\widehat{COE}\)
Ta có : \(\widehat{BOE}\) và \(\widehat{BOD}\) kề bù nên \(\widehat{BOE}+\widehat{BOD}=180^o\)
\(\Rightarrow\text{ }\widehat{BOE}+135^o=180^o\text{ }\Rightarrow\text{ }\widehat{BOE}=45^o\)
Ta lại có : \(\widehat{COD}+\widehat{COE}=180^o\)
\(\widehat{COD}+90^o=180^o\)
\(\widehat{COD}=90^o\)
\(\text{ }\Rightarrow\text{ }OC\perp OE\)

a) Ta có:
\(\widehat{DOA}=\widehat{COB}\left(=160^o-\widehat{DOC}\right)\) (1)
Mà \(\widehat{DOA}=\widehat{EOB}\) (2 góc đối đỉnh) (2)
Từ (1) và (2) \(\Rightarrow\widehat{COB}=\widehat{BOE}\left(đpcm\right)\)
b) Vì \(\widehat{COB}=\widehat{BOE}\) (cmt)
\(\Rightarrow OB\) là phân giác của \(\widehat{COE}\)

Ta có : Góc COA = góc AOE ; góc BOD = góc BOF
Mà góc BOD + góc COD + góc COA = 180 độ ; góc AOE + góc EOF + góc BOF = 180 độ
=> góc COD = góc EOF = 90 độ
=> OE vuông góc với OF

Do OC vuông góc với OD
\(\Rightarrow\widehat{COD}=90^o\)
Do OA là tia p.g của \(\widehat{COE}\)
OB là tia p.g của \(\widehat{DOF}\)
\(\Rightarrow\widehat{COD}\)đối đỉnh \(\widehat{EOF}\)
mà \(\widehat{COD}=90^o\)
\(\Rightarrow\widehat{EOF}=90^o\)
mà góc EOF = \(90^o\)
\(\Rightarrow\)OE vuông góc OF
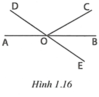
Hai góc AOC và BOC kề bù nên A O C ^ + B O C ^ = 180 °
⇒ B O C ^ = 180 ° − 150 ° = 30 ° .
Tương tự, ta tính được A O D ^ = 30 ° .
Ta có B O E ^ = A O D ^ = 30 ° (hai góc đối đỉnh).
Suy ra B O C ^ = B O E ^ = 30 ° . (1)
Tia OB nằm giữa hai tia OC và OE. (2)
Từ (1) và (2) ta được tia OB là tia phân giác của góc COE
Đếm góc, đếm tia