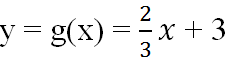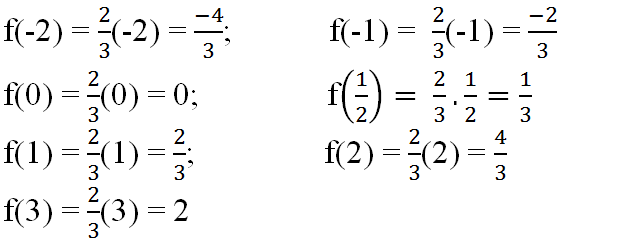Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn kiểm tra lại đề, \(f\left(x\right)=\dfrac{x^3}{1-3x-3x^2}\) hay \(f\left(x\right)=\dfrac{x^3}{1-3x+3x^2}\)

Ta xét : \(f\left(x\right)+f\left(1-x\right)=\frac{x^3}{1-3x+3x^2}+\frac{\left(1-x\right)^3}{1-3\left(1-x\right)+3\left(1-x\right)^2}\)
\(=\frac{x^3}{1-3x+3x^2}+\frac{\left(1-x\right)^3}{3x^2-3x+1}=\frac{\left(x+1-x\right)\left(x^2+x^2-2x+1+x^2-x\right)}{3x^2-3x+1}=\frac{3x^2-3x+1}{3x^2-3x+1}=1\)
Áp dụng ta có :
\(A=\left[f\left(\frac{1}{2012}\right)+f\left(\frac{2011}{2012}\right)\right]+\left[f\left(\frac{2}{2012}\right)+f\left(\frac{2010}{2012}\right)\right]+...+\left[f\left(\frac{1006}{2012}\right)+f\left(\frac{1006}{2012}\right)\right]\)
\(=1+1+...+1\)(Có tất cả 1006 số 1)
\(=1006\)

Đễ dàng chưng minh được
\(f\left(1-x\right)=1-f\left(x\right)\)
\(\Rightarrow f\left(1-x\right)+f\left(x\right)=1\)
\(\Rightarrow A=\left[f\left(\frac{1}{2012}\right)+f\left(\frac{2011}{2012}\right)\right]+\left[f\left(\frac{2}{2012}\right)+f\left(\frac{2010}{2012}\right)\right]+...+\left[f\left(\frac{1005}{2012}\right)+f\left(\frac{1007}{2012}\right)\right]+f\left(\frac{1006}{2012}\right)\)
\(=1005+f\left(\frac{1006}{2012}\right)\)
Làm nôt

Lời giải:
Ta thấy: \(f(x)=\frac{x^3}{1-3x+3x^2}\Rightarrow f(1-x)=\frac{(1-x)^3}{1-3(1-x)+3(1-x)^2}=\frac{(1-x)^3}{3x^2-3x+1}\)
\(\Rightarrow f(x)+f(1-x)=\frac{x^3}{1-3x+3x^2}+\frac{(1-x)^3}{3x^2-3x+1}=\frac{x^3+(1-x)^3}{3x^2-3x+1}=1\)
Do đó:
\(f\left(\frac{1}{2017}\right)+f\left(\frac{2016}{2017}\right)=1\)
\(f\left(\frac{2}{2017}\right)+f\left(\frac{2015}{2017}\right)=1\)
............
\(f\left(\frac{1008}{2017}\right)+f\left(\frac{1009}{2017}\right)=1\)
Cộng theo vế:
\(\Rightarrow A=f\left(\frac{1}{2017}\right)+f\left(\frac{2}{2017}\right)+f\left(\frac{3}{2017}\right)+...f\left(\frac{2015}{2017}\right)+f\left(\frac{2016}{2017}\right)\)
\(=\underbrace{1+1+1...+1}_{1008}=1008\)

\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{20a-11}{2012}\\x_1x_2=-1\end{matrix}\right.\)
\(P=\dfrac{3}{2}\left(x_1-x_2\right)^2+2\left(\dfrac{x_1-x_2}{2}-\dfrac{x_1-x_2}{x_1x_2}\right)^2\)
\(=\dfrac{3}{2}\left(x_1-x_2\right)^2+2\left(x_1-x_2\right)^2\left(\dfrac{1}{2}-\dfrac{1}{x_1x_2}\right)^2\)
\(=\dfrac{3}{2}\left(x_1-x_2\right)^2+2\left(x_1-x_2\right)^2\left(\dfrac{1}{2}+1\right)^2\)
\(=6\left(x_1-x_2\right)^2=6\left(x_1+x_2\right)^2-24x_1x_2\)
\(=6\left(\dfrac{20a-11}{2012}\right)^2+24\ge24\)
Dấu "=" xảy ra khi \(a=\dfrac{11}{20}\)

c) Từ kết quả câu a, b ta được bảng sau:
Nhận xét:
- Các hàm số y = f(x) = 2/3 x và y = g(x) = 2/3 x + 3 là hai hàm số đồng biến vì khi x tăng thì y cũng nhận được các giá trị tương ứng tăng lên.
- Cùng một giá trị của biến x, giá trị của hàm số y = g(x) luôn luôn lớn hơn giá trị tương ứng của hàm số y = f(x) là 3 đơn vị.
a) Cho hàm số : \(y=f\left(x\right)=\dfrac{2}{3}x\)
Ta có : \(f\left(-2\right)=\dfrac{2}{3}.\left(-2\right)=-\dfrac{4}{3}\)
\(f\left(-1\right)=\dfrac{2}{3}.\left(-1\right)=-\dfrac{2}{3}\)
\(f\left(0\right)=\dfrac{2}{3}.0=0\)
\(f\left(\dfrac{1}{2}\right)=\dfrac{2}{3}.\dfrac{1}{2}=\dfrac{1}{3}\)
\(f\left(1\right)=\dfrac{2}{3}.1=\dfrac{2}{3}\)
\(f\left(2\right)=\dfrac{2}{3}.2=\dfrac{4}{3}\)
\(f\left(3\right)=\dfrac{2}{3}.3=2\)
b) Cho hàm số : \(y=g\left(x\right)=\dfrac{2}{3}x+3\)
\(g\left(-2\right)=\dfrac{2}{3}.\left(-2\right)+3=\dfrac{5}{3}\)
\(g\left(-1\right)=\dfrac{2}{3}.\left(-1\right)+3=\dfrac{7}{3}\)
\(g\left(0\right)=\dfrac{2}{3}.0+3=3\)
\(g\left(\dfrac{1}{2}\right)=\dfrac{2}{3}.\dfrac{1}{2}+3=\dfrac{10}{3}\)
\(g\left(1\right)=\dfrac{2}{3}.1+3=\dfrac{11}{3}\)
\(g\left(2\right)=\dfrac{2}{3}.2+3=\dfrac{13}{3}\)
\(g\left(3\right)=\dfrac{2}{3}.3+3=5\)
c) Khi \(x\)lấy cùng một giá trị thì giá trị của \(g\left(x\right)\) lớn hơn giá trị của \(f\left(x\right)\) là \(3\) đơn vị.

d) Ta có: \(D=\left(\dfrac{5\sqrt{x}-6}{x-9}-\dfrac{2}{\sqrt{x}+3}\right):\left(1+\dfrac{6}{x-9}\right)\)
\(=\dfrac{5\sqrt{x}-6-2\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}:\dfrac{x-9+6}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{5\sqrt{x}-6-2\sqrt{x}+6}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{x-3}\)
\(=\dfrac{3\sqrt{x}}{x-3}\)
f) Ta có: \(\left(\dfrac{3}{\sqrt{1+x}}+\sqrt{1-x}\right):\left(\dfrac{3}{\sqrt{1-x^2}}+1\right)\)
\(=\dfrac{3+\sqrt{1-x^2}}{\sqrt{1+x}}:\dfrac{3+\sqrt{1-x^2}}{\sqrt{1-x^2}}\)
\(=\dfrac{\sqrt{1-x^2}}{\sqrt{1+x}}=\sqrt{1-x}\)

a)đk:`2x-4>=0`
`<=>2x>=4`
`<=>x>=2.`
b)đk:`3/(-2x+1)>=0`
Mà `3>0`
`=>-2x+1>=0`
`<=>1>=2x`
`<=>x<=1/2`
c)`đk:(-3x+5)/(-4)>=0`
`<=>(3x-5)/4>=0`
`<=>3x-5>=0`
`<=>3x>=5`
`<=>x>=5/3`
d)`đk:-5(-2x+6)>=0`
`<=>-2x+6<=0`
`<=>2x-6>=0`
`<=>2x>=6`
`<=>x>=3`
e)`đk:(x^2+2)(x-3)>=0`
Mà `x^2+2>=2>0`
`<=>x-3>=0`
`<=>x>=3`
f)`đk:(x^2+5)/(-x+2)>=0`
Mà `x^2+5>=5>0`
`<=>-x+2>0`
`<=>-x>=-2`
`<=>x<=2`
a, ĐKXĐ : \(2x-4\ge0\)
\(\Leftrightarrow x\ge\dfrac{4}{2}=2\)
Vậy ..
b, ĐKXĐ : \(\left\{{}\begin{matrix}\dfrac{3}{-2x+1}\ge0\\-2x+1\ne0\end{matrix}\right.\)
\(\Leftrightarrow-2x+1>0\)
\(\Leftrightarrow x< \dfrac{1}{2}\)
Vậy ..
c, ĐKXĐ : \(\dfrac{-3x+5}{-4}\ge0\)
\(\Leftrightarrow-3x+5\le0\)
\(\Leftrightarrow x\ge\dfrac{5}{3}\)
Vậy ...
d, ĐKXĐ : \(-5\left(-2x+6\right)\ge0\)
\(\Leftrightarrow-2x+6\le0\)
\(\Leftrightarrow x\ge-\dfrac{6}{-2}=3\)
Vậy ...
e, ĐKXĐ : \(\left(x^2+2\right)\left(x-3\right)\ge0\)
\(\Leftrightarrow x-3\ge0\)
\(\Leftrightarrow x\ge3\)
Vậy ...
f, ĐKXĐ : \(\left\{{}\begin{matrix}\dfrac{x^2+5}{-x+2}\ge0\\-x+2\ne0\end{matrix}\right.\)
\(\Leftrightarrow-x+2>0\)
\(\Leftrightarrow x< 2\)
Vậy ...