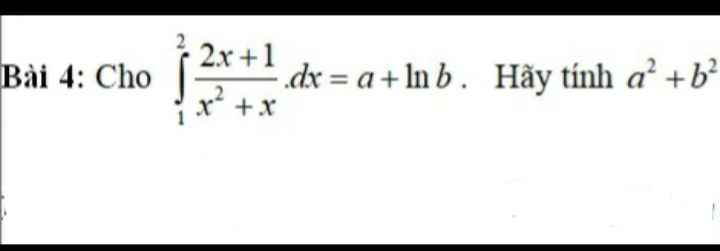Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Có: \(I=\int\limits^{ln3}_0\sqrt{e^x-1}e^xdx\)
Đặt \(t=\sqrt{e^x-1}\Rightarrow t^2=e^x-1\)
\(\Rightarrow2tdt=e^xdx\)
\(\Rightarrow I=\int\limits^{\sqrt{2}}_02t^2dt\) \(\Rightarrow I=\dfrac{2}{3}t^3|^{\sqrt{2}}_0=\dfrac{4}{3}\sqrt{2}\)
Vậy a=0, b=\(\dfrac{4}{3}\) \(\Rightarrow a+b=0+\dfrac{4}{3}=\dfrac{4}{3}\)



\(\int\limits^2_1\dfrac{2x+1}{x^2+x}dx=\int\limits^2_1\dfrac{d\left(x^2+x\right)}{x^2+x}=ln\left(x^2+x\right)|^2_1=ln6-ln2=ln3\)
\(\Rightarrow\left\{{}\begin{matrix}a=0\\b=3\end{matrix}\right.\) \(\Rightarrow a^2+b^2=9\)

Người ta có cho hàm f(x) là gì hay tích phân của hàm f(x) bằng bao nhiêu ko ?

Đặt \(z=x+yi\)
\(\dfrac{\left(x+yi\right)\left(1+i\right)}{2}+\left(x-yi\right)\left(5+2i\right)=31-17i\)
\(\Leftrightarrow x-y+\left(x+y\right)i+10x+4xi-10yi+4y=31-17i\)
\(\Leftrightarrow\left(11x+3y\right)+\left(5x-9y\right)i=62-34i\)
\(\Leftrightarrow\left\{{}\begin{matrix}11x+3y=62\\5x-9y=-34\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=4\\y=6\end{matrix}\right.\)

Lời giải:
a. Sau 2 năm thu được:
$100(1+\frac{0,5}{100})^{24}=112,72$ (triệu đồng)
b.
Giả sử sau $n$ tháng thì rút ra được gốc lẫn lãi là 300 triệu
$100(1+0,005)^n=300$
$1,005^n=3$
$n=\log_{1,005}3=220,3$ (tháng)
Vậy sau ít nhất 221 tháng thì người đó rút được 300 triệu. Đổi 221 tháng thành 18 năm 5 tháng
Đáp án C.


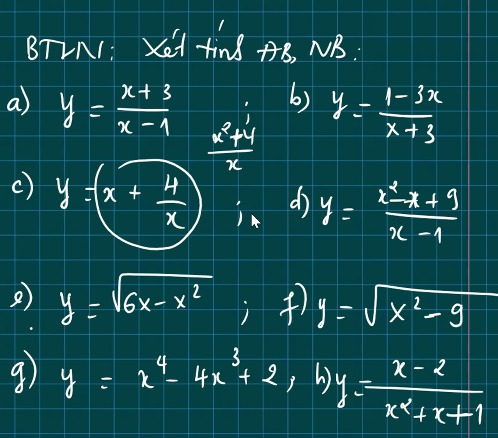 Cho em xin lời giải chi tiết với ạ
Cho em xin lời giải chi tiết với ạ