
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C.
Ta có: y ' = x 2 + 2 mc + 2 m - 1 . Để hàm số có cực trị thì phương trình y'= 0 có hai nghiệm phân biệt
⇔ Δ ' > 0 ⇔ m 2 - 2 m + 1 > 0 ⇔ ( m - 1 ) 2 > 0 ⇔ m ≠ 1 .

Đáp án A
Phương pháp giải:
Tìm tọa độ điểm cực trị của đồ thị hàm số trùng phương và tính diện tích tam giác
Lời giải: TXĐ : D = R
Ta có ![]() R
R
Phương trình 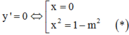
Hàm số có 3 điểm cực trị ó (*) có 2 nghiệm phân biệt khác ![]()
Khi đó 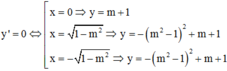
Gọi ![]() ;
; ![]() là ba điểm cực trị. Tam giác ABC cân tại A.
là ba điểm cực trị. Tam giác ABC cân tại A.
Trung điểm H của BC là ![]()
![]()
Và ![]()
Diện tích tam giác ABC là ![]()
![]()
Mà ![]() R suy ra
R suy ra ![]()
Vậy Smax = 1 Dấu bằng xảy ra khi và chỉ khi m = 0

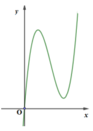

Để đồ thị hàm số có 2 điểm cực trị thì
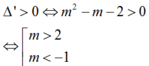
Khi đó, do a = 1 3 > 0 nên hàm số y = 1 3 x 3 - m x 2 + m + 2 x có cực trị và giá trị của hàm số tại các điểm cực đại, điểm cực tiểu nhận giá trị dương . Đồ thị hàm số cắt trục hoành tại 1 điểm duy nhất là x = 0 1 và hai cực trị x 1 ; x 2 x 1 < x 1 thỏa mãn: 0 < x 1 < x 2 2
Ta có:
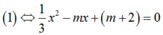
hoặc là vô nghiệm hoặc là có nghiệm kép x = 0
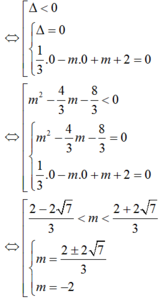
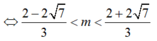
Kết hợp điều kiện ta có:
m ∈ 2 - 2 7 3 ; - 1 ∪ 2 ; 2 + 2 7 3
Chọn: A

Đáp án B.
Ta có y ' = 2 x 2 + 2 m + 1 x + m 2 + 4 m + 3 ; ∀ x ∈ ℝ .
Phương trình y ' = 0 ⇔ 2 x 2 + 2 m + 1 x + m 2 + 4 m + 3 = 0 (*).
Để hàm số đã cho có 2 điểm cực trị ⇔ (*) có 2 nghiệm phân biệt ⇔ ∆ ' > 0 ⇔ - 5 < m < - 1 .
Và các điểm cực trị của hàm số nằm bên phải Oy ⇔ m 2 + 4 m + 3 > 0 ⇔ [ m > - 1 m < - 3 .
Vậy - 5 < m < - 3 là giá trị cần tìm.

Đáp án A.
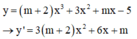
Hàm số đã cho có điểm cực đại và điểm cực tiểu đều có hoành độ dương

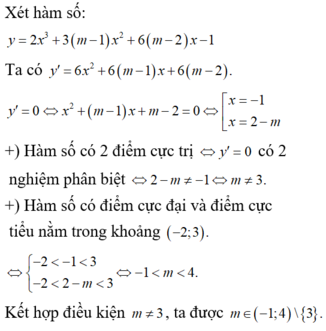

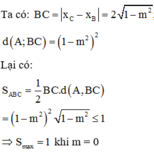

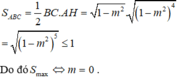
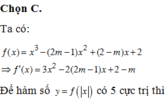

để hàm số f có cực trị tại a thì f'(\(x_0\))=0
để tìm cực trị của hàm số thì có 2 quy tắc
1, quy tắc 1
f liên tục trên (a,b) chữa điểm a và có đạo hàm trên các khoảng (a;\(x_0\)) và (\(x_0\),b). Khi đó
a, nếu f'(x)<0 với mọi \(x\in\) (a;\(x_0\)) và f'(\(x_0\))>0 với mọi \(x\in\left(x_0;b\right)\) thì hàm số f đạt cực tiểu tại điểm \(x_0\)
b, nếu f'(x)>0 với mọi \(x\in\) (a;\(x_0\)) và f'(\(x_0\))<0 với mọi \(x\in\left(x_0;b\right)\) thì hàm số f đạt cực đại tại điểm \(x_0\)
quy tắc 1
bước 1. tìm f'(x)
bước 2:tìm các điểm \(x_i\) tại đó đạo hàm của nó =0 hoặc hàm số liên tục nhưng ko có đạo hàm
bước 3: xét dấu f'(x). nếu f'(x) đổi dấu khi qua điểm xi thì hàm số đặt cực trị tại xi
Gỉa sử f có đạo hàm cấp 1 trên khoảng (a,b) chứa điểm x0 , f'(x0)=0 f có đạo hàm cấp hai khác 0 tại điểm x0
a, nếu f''(x0)<0 thì hàm số đạt cực đại tại x0
b, nếu f''(x0)>0 thì hàm số đạt cực tiểu tại x0
quy tắc 2:
bước 1: tìm f'(x)
tìm các nghiệm của phương trình f'(xi)=0
bước 3: tìm f''(x) và tính f''(xi)
nếu f''(xi)<0 thì hàm số đạt cực đại tại xi
nếu f''(xi)>0 thì hàm số đạt cực đại tại xi