Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, HS tự làm
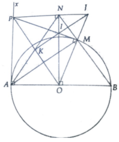
b, Ta có OP ⊥ AM, BM ⊥ AM => BM//OP
c, chứng minh ∆AOP = ∆OBN => OP=BN
lại có BN//OP do đó OPNB là hình bình hành
d, Ta có ON ⊥ PI, PM ⊥ JO mà PM ∩ ON = I => I là trực tâm ∆POJ => JI ⊥ PO(1)
Chứng minh PAON hình chữ nhật => K trung điểm PO
Lại có A P O ^ = O P I ^ = I O P ^ => ∆IPO cân tại I => IKPO (2)
Từ (1),(2) => J,I,K thẳng hàng

a) Xét (O) có
NA là tiếp tuyến có A là tiếp điểm(gt)
NE là tiếp tuyến có E là tiếp điểm(gt)
Do đó: ON là tia phân giác của \(\widehat{AOE}\)(Tính chất hai tiếp tuyến cắt nhau)
hay \(\widehat{AOE}=2\cdot\widehat{EON}\)
Xét (O) có
ME là tiếp tuyến có E là tiếp điểm(gt)
MB là tiếp tuyến có B là tiếp điểm(gt)
Do đó: OM là tia phân giác của \(\widehat{EOB}\)(Tính chất hai tiếp tuyến cắt nhau)
hay \(\widehat{EOB}=2\cdot\widehat{EOM}\)
Ta có: \(\widehat{EOA}+\widehat{EOB}=180^0\)(hai góc kề bù)
hay \(2\cdot\widehat{EON}+2\cdot\widehat{EOM}=180^0\)
\(\Leftrightarrow\widehat{EON}+\widehat{EOM}=90^0\)
hay \(\widehat{MON}=90^0\)(đpcm)
b) Áp dụng hệ thức lượng trong tam giác vuông vào \(\Delta\)ONM vuông tại O có OE là đường cao ứng với cạnh huyền NM, ta được:
\(ME\cdot NE=OE^2\)
mà OE=R
nên \(ME\cdot NE=R^2\)(đpcm)

a: Xét tứ giác OACM có
\(\widehat{OAC}+\widehat{OMC}=90^0+90^0=180^0\)
=>OACM là tứ giác nội tiếp
=>O,A,C,M cùng thuộc một đường tròn
b: Xét (O) có
CA,CM là tiếp tuyến
Do đó: CA=CM
=>C nằm trên đường trung trực của AM(1)
OA=OM
=>O nằm trên đường trung trực của AM(2)
Từ (1) và (2) suy ra OC là đường trung trực của AM
=>OC\(\perp\)AM
Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>AM\(\perp\)MB tại M
Ta có: AM\(\perp\)MB
AM\(\perp\)OC
Do đó: OC//MB
c: Xét (O) có
ΔAKB nội tiếp
AB là đường kính
Do đó: ΔAKB vuông tại K
=>KB\(\perp\)KA tại K
=>AK\(\perp\)BC tại K
Xét ΔABC vuông tại A có AK là đường cao
nên \(BK\cdot BC=BA^2=\left(2R\right)^2=4R^2\)

a: góc OAC+góc OMC=180 độ
=>OACM nội tiếp
b: góc BOM=2*60=120 độ
=>góc BDM=60 độ
=>ΔBMD đều
\(S_{qMB}=\dfrac{pi\cdot R^2\cdot120}{360}=\dfrac{1}{3}\cdot pi\cdot R^2\)

a: Xét tứ giác OAPC có
góc OAP+góc OCP=180 độ
nên OAPC là tứ giác nội tiếp
b: Xét (O) có
PC,PA là tiếp tuyến
nên PA=PC
mà OC=OA
nên OP là trung trực của AC
=>OP vuông góc với AC
Xét (O) có
QC,QB là các tiếp tuyến
nên QC=QB
mà OB=OC
nên OQ là trung trực của BC
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đo: ΔACB vuông tại C
Xét tứ giác CMON có
góc CMO=góc CNO=góc MCN=90 độ
nen CMON là hình chữ nhật
c: PA*BQ=PC*CQ=OC^2=OB*OA

Bạn có thể tham khảo bài tương tự ở đây:
BT: Cho nửa đường tròn (O;R) đường kính AB. Kẻ 2 tiếm tuyến Ax, By của nửa đường tròn (O). Qua M thuộc nửa đường tròn (... - Hoc24
CM góc COD = 90 độ
Theo tính chất 2 tiếp tuyến cắt nhau
Ta có : OC là phân giác góc AOM
=> góc COM = 1/2 góc AOM
OD là phân giác góc BOM
=> góc DOM = 1/2 góc BOM
=> góc COD = góc COM + góc DOM = 1/2 ( góc AOM + góc BOM ) = 1/2 góc AOB = 1/2 x 180 độ = 90 độ



