Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: \(\widehat{CHB}=90^0\)
=>ΔCHB vuông tại H
=>ΔCHB nội tiếp đường tròn đường kính CB(4)
Ta có: \(\widehat{CKB}=90^0\)
=>ΔCKB vuông tại K
=>ΔCKB nội tiếp đường tròn đường kính CB(5)
Từ (4) và (5) suy ra C,H,B,K cùng thuộc đường tròn đường kính CB
b:
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Ta có: \(\widehat{OCB}+\widehat{BCK}=\widehat{OCK}=90^0\)
\(\widehat{OCB}+\widehat{OCA}=\widehat{BCA}=90^0\)
Do đó: \(\widehat{BCK}=\widehat{OCA}\)(1)
Ta có: CHBK là tứ giác nội tiếp
=>\(\widehat{BCK}=\widehat{BHK}\left(2\right)\)
Xét ΔOAC có OC=OA
nên ΔOAC cân tại O
=>\(\widehat{OAC}=\widehat{OCA}\)(3)
Từ (1),(2),(3) suy ra \(\widehat{BHK}=\widehat{OAC}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên HK//AC

a, ta có: góc AEI = 90o (góc nội tiếp chắn nửa đường tròn) => EI\(\perp\)AK tại E và AH\(\perp\)KI tại H (gt)
chúng cắt nhau tại B => B là trực tâm. => KB vuông góc AI (đpm)
b, ta có: góc ECA = góc EBA ( cùng chắn cung AE) mà góc EBA= góc HBI (hai góc đối đỉnh) (4)
ta lại có: góc HBI + góc HIB =90o (tổng 3 góc trong một tam giác) (3)
=> góc ECA + góc HIB = 90o (1)
Xét tam giác CEI vuông tại E nên: góc EKI + góc HIB =90o (2)
Từ (1) và (2) => góc ECA = góc EKI
=> tứ giác EKNC là tứ giác nội tiếp ) (đpcm)
c,Ta có: góc EAB + góc EBA = 90o và từ (3), (4) => góc EAB = góc BIH
mà góc EAB = góc BEN ( bằng 1/2 sđ cung EB)
=> góc BIH = góc BEN=> tam giác ENI cân tại N=> EN =NI (*)
Tương tự, ta có góc K + góc KAH = 90o
góc KEN + góc NEB =90o mà góc KAH = góc NEB (c.m.t) => góc KEN = góc K => tam giác KNE cân tại N => NK = NE (**)
từ (*) và (**) => NK = NI hay N là trung điểm KI ( đpcm)

Tôi cũng có bài khó giống ý hệt bạn,vậy bạn có hướng làm chưa

a: góc MHO+góc MKO=180 độ
=>MHOK nội tiêp
C,N,D,F cùng thuộc (O)
nên CNDF nội tiếp
b: Xét ΔCKM vuông tại K và ΔCHO vuông tại H có
góc KCM chung
=>ΔCKM đồng dạng voi ΔCHO
=>CK/CH=CM/CO
=>CK*CO=CH*CM

Bạn tự vẽ hình nha:
a)Ta có: gócBCD=gócA (cùng chắn cung BC); gócBCE=gócA (cùng phụ với góc CBA) => CB là pg DCE
b)Vì CB là pg DCE hay CB là pg KCH mà BK vuông góc CK; BH vuông góc CH => BK=BH => BK+BD=BD+BH=DH<ED (quan hệ giữa đường vuông góc với đường xiên)
c)Vì CB là pg của tam giác CDH => BH/BD=CH/CD (1); Mà CB vuông góc CA => Ca là pg ngoài tại C của tam giác CDH => AH/AD=CH/CD (2) .
Từ (1) và (2) suy ra: BH/BD=AH/AD (=CH/CD) <=> BH.AD=AH.BD

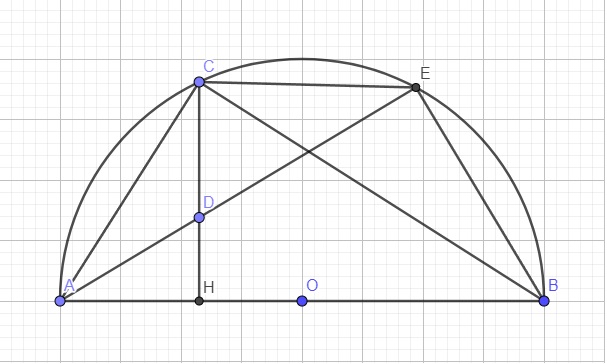
a.
\(DH\perp AB\left(gt\right)\Rightarrow\widehat{DHB}=90^0\Rightarrow D;H;B\) cùng thuộc đường tròn đường kính DB
\(\widehat{AEB}=90^0\) (góc nội tiếp chắn nửa đường tròn (O)) \(\Rightarrow\widehat{DEB}=90^0\)
\(\Rightarrow D;E;B\) cùng thuộc đường tròn đường kính DB
\(\Rightarrow\) Tứ giác BHDE nội tiếp đường tròn đường kính DB
b.
\(\widehat{ACB}=90^0\) (góc nội tiếp chắn nửa đường tròn (O))
\(\Rightarrow\widehat{ACH}=\widehat{ABC}\) (cùng phụ \(\widehat{BAC}\))
Mà \(\widehat{ABC}=\widehat{AEC}\) (cùng chắn cung AC của (O)
\(\Rightarrow\widehat{ACH}=\widehat{AEC}\)
Xét hai tam giác ADC và ACE có: \(\left\{{}\begin{matrix}\widehat{ACH}=\widehat{AEC}\left(cmt\right)\\\widehat{CAD}\text{ chung}\end{matrix}\right.\)
\(\Rightarrow\Delta ADC\sim\Delta ACE\left(g.g\right)\Rightarrow\dfrac{AD}{AC}=\dfrac{CD}{EC}\Rightarrow AD.EC=CD.AC\)
c.
Cũng theo cmt \(\Delta ADC\sim\Delta ACE\Rightarrow\dfrac{AC}{AE}=\dfrac{AD}{AC}\Rightarrow AD.AE=AC^2\)
Áp dụng hệ thức lượng trong tam giác vuông ABC với đường cao CH:
\(BC^2=BH.BA\)
\(\Rightarrow AD.AE+BH.BA=AC^2+BC^2=AB^2=2022^2\)
Xét tứ giác CHBK có
\(\widehat{CHB}+\widehat{CKB}=90^0+90^0=180^0\)
=>CHBK là tứ giác nội tiếp
=>C,H,B,K cùng thuộc một đường tròn
Bạn vẽ hộ mình và cm theo tam giác nội tiếp