Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) Trong (O) có BC là dây cung không đi qua O,có H là trung điểm BC
\(\Rightarrow OH\bot BC\Rightarrow\angle OHA=90\) mà \(\angle OMA=90\Rightarrow OMAH\) nội tiếp
2) Ta có: \(\Delta AMO\) vuông tại M có \(AO\bot MI\Rightarrow AM^2=AI.AO\)
1.
Theo giả thiết: \(H\) là trung điểm BC
\(\Rightarrow OH\perp BC\Leftrightarrow\widehat{OHA}=90^o\)
Lại có: \(AM\perp OM\Leftrightarrow\widehat{OMA}=90^o\)
\(\Rightarrow\widehat{OHA}+\widehat{OMA}=180^o\)
\(\Rightarrow AMOH\) nội tiếp
Hay \(A,M,O,H\) cùng thuộc đường tròn đường kính OA

a, b, c HS tự làm
d, Gợi ý: G' ÎOI mà I G ' I O = 1 3 => G' thuộc (G'; 1 3 R)

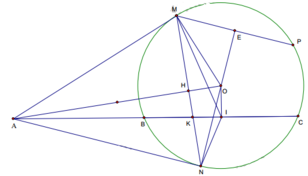
Theo giả thiết AMO = ANO = AIO = 90o = > 5 điểm A, O, M, N, I thuộc đường tròn đường kính AO 0,25
=> AIN = AMN, AIM = ANM (Góc nội tiếp cùng chắn một cung)
AM = AN => ∆AMN cân tại A => AMN = ANM
=> AIN = AIM => đpcm

2 A K = 1 A B + 1 A C ⇔ 2 A B . A C = A K ( A B + A C ) ⇔ A B . A C = A K . A I
(Do AB+ AC = 2AI)
∆ABN đồng dạng với ∆ANC => AB.AC = AN2
∆AHK đồng dạng với ∆AIO => AK.AI = AH.AO
Tam giác ∆AMO vuông tại M có đường cao MH => AH.AO = AM2
=> AK.AI = AM2 . Do AN = AM => AB.AC = AK.AI


a, Chú ý: A M O ^ = A I O ^ = A N O ^ = 90 0
b, A M B ^ = M C B ^ = 1 2 s đ M B ⏜
=> DAMB ~ DACM (g.g)
=> Đpcm
c, AMIN nội tiếp => A M N ^ = A I N ^
BE//AM => A M N ^ = B E N ^
=> B E N ^ = A I N ^ => Tứ giác BEIN nội tiếp => B I E ^ = B N M ^
Chứng minh được: B I E ^ = B C M ^ => IE//CM
d, G là trọng tâm DMBC Þ G Î MI
Gọi K là trung điểm AO Þ MK = IK = 1 2 AO
Từ G kẻ GG'//IK (G' Î MK)
=> G G ' I K = M G M I = M G ' M K = 2 3 I K = 1 3 A O không đổi (1)
MG' = 2 3 MK => G' cố định (2). Từ (1) và (2) có G thuộc (G'; 1 3 AO)
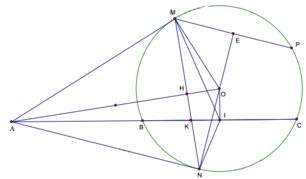
1, Xét $(O)$ có các tiếp tuyến $AM;AN$
suy ra $\widehat{AMO}=\widehat{ANO}=90^o;AM=AN;AO$ là phân giác $\widehat{MAN}$
nên $\widehat{AMO}+\widehat{ANO}=180^o$
suy ra tứ giác $AMON$ nội tiếp (tổng 2 góc đối =180 độ)
2, Ta có: $AM=AN⇒ΔAMN$ cân tại $A$
có đường phân giác $AO$
$⇒AO$ đồng thời là đường trung trực tam giác $AMN$
$⇒AO⊥MN$ tại $H$
3. Xét $ΔAMO$ vuông tại $M$
$MH$ là đường cao
Nên $AH.AO=AM^2$ (hệ thức lượng trong tam giác vuông)
Xét $(O)$ có: Tiếp tuyến $AM$
nên $\widehat{AMB}=\widehat{MCB}$ (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung $BM$)
hay $\widehat{AMB}=\widehat{ACM}$
Xét tam giác $AMB$ và tam giác $ACM$ có:
$\widehat{AMB}=\widehat{ACM}$
$\widehat{A}$ chung
Nên tam giác $AMB$ và tam giác $ACM$ đồng dạng (g.g)
suy ra $\dfrac{AB}{AM}=\dfrac{AM}{AC}$
nên $AM^2=AB.AC$
Từ đó suy ra $AH.AO=AB.AC$
hình đâu bn ơi