Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

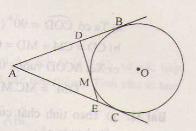
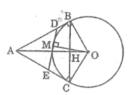
Chứng minh AB=AC; DB=DM và EC=EM.
Chu vi ΔADE bằng
= AD + DM + ME + AE
= AD + DB + EC + AE
= AB + AC
= 2AB.
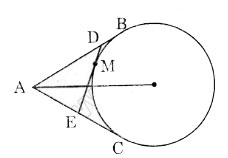
Ta có AB = AC; DB = DM;
EC = EM.
Chu vi Δ ADE:
AD +AE +DE = AD +DM + AE + EM
=AD + DB + AE + EC = AB + AC = 2AB

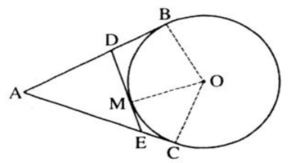
Theo tính chất hai tiếp tuyến cắt nhau ta có:
DM = DB, EM = EC, AB = AC
Chu vi ΔADE:
CΔADE = AD + DE + AE = AD + DM + ME + AE = AD + DB + EC + AE = AB + AC = 2AB (đpcm)

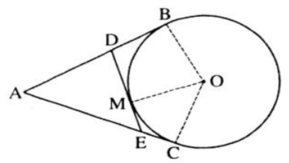
Theo tính chất hai tiếp tuyến cắt nhau ta có:
DM = DB, EM = EC, AB = AC
Chu vi ΔADE:
CΔADE = AD + DE + AE = AD + DM + ME + AE = AD + DB + EC + AE = AB + AC = 2AB (đpcm)

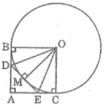
Áp dụng định lí Pitago vào tam giác vuông ABO, ta có:
A O 2 = A B 2 + B O 2
Suy ra: A B 2 = A O 2 - B O 2 = 5 2 - 3 2 = 16
AB = 4 (cm)
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
DB = DM
EM = EC
Chu vi của tam giác ADE bằng:
AD + DE + EA = AD + DB + AE + EC
= AB + AC = 2AB = 2.4 = 8 (cm)

Theo tính chất của hai tiếp tuyến cắt nhau ta có :
DB = DM
EM = EC
Chu vi của tam giác ADE bằng :
AD + DE + EA = AD + DM + ME + EA
= AD + DB + AE + EC = AB + AC = 2AB
Mà tứ giác ABOC là hình vuông (chứng minh trên) nên:
AB = OB = 2 (cm)
Vậy chu vi của tam giác ADE bằng: 2.2 = 4 (cm)

a) C/m tg ABCO nội tiếp:
+) Ta có: góc ACO = 90•( vì AC là tiếp tuyến đg tròn (O))
góc ABO = 90•( vì AB là tiếp tuyến đg tròn (O))
+) Xét tg ABOC có: góc ACO+ góc ABO=90•+90•=180•
Mà 2 góc ở vị trí đối nhau
=> tg ABOC nội tiếp đg tròn(dhnb)
b) C/m: CD// AO:
+) Vì AB và AC là 2 tiếp tuyến cắt nhau tại A(gt) => AO là đg pg của góc COB( t/c 2 tiếp tuyến cắt nhau)
=> AO là pg của tam giác COB
Mà tam giác COB cân tại O( OB=OC=R)
=> OA là đg cao của tam giác COB( t/c tam giác cân)
=> OA vuông góc vs CB( t/c) (1)
+) Xét (O) ta có:
BD là đg kính( gt)
góc BCD là góc nội tiếp chắn cung BD
=> góc BCD= 90• ( t/c góc nội tiếp chắn nửa đg tròn)
=> CD vuông góc vs CB(t/c) (2)
Từ(1) và (2) suy ra: CD// OA( từ vuông góc đến song song).
mk chưa ra câu c nên xin lỗi bn nhiều nhé....