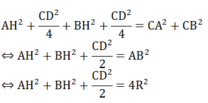Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
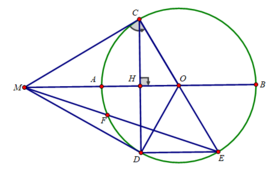
b) Ta có: OM = OA + AM = R + R = 2R
Xét tam giác MCO vuông tại C, CH là đường cao có:
MO 2 = MC 2 + OC 2
CH.OM = CM.CO
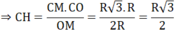
Lại có: CD = 2CH ⇒ CD = R 3
Tam giác CDE nội tiếp (O) có CE là đường kính nên ΔCDE vuông tại D
Theo định lí Py ta go ta có:
CE 2 = CD 2 + DE 2
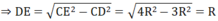
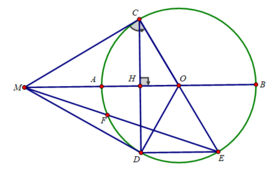
a) Xét tam giác COD cân tại O có OH là đường cao
⇒ OH cũng là tia phân giác ⇒ ∠(COM) = ∠(MOD)
Xét ΔMCO và ΔMOD có:
CO = OD
∠(COM) = ∠(MOD)
MO là cạnh chung
⇒ ΔMCO = ΔMOD (c.g.c)
⇒ ∠(MCO) = ∠(MDO)
∠(MCO) = 90 0 nên ∠(MDO) = 90 0
⇒ MD là tiếp tuyến của (O)
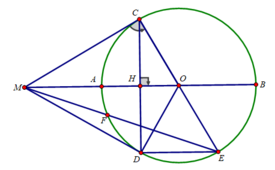
d) Ta có: ∠(CFE) = 90 0 (F thuộc đường tròn đường kính CE)
Lại có CF là đường cao nên MC 2 = MF.ME
Tương tự, ta có: MC 2 = MH.MO
⇒ ME.MF = MH.MO
⇒
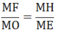
Xét ΔMOF và ΔMEN có:
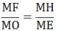
∠(FMO) chung
⇒ ΔMOF ∼ ΔMEN (c.g.c)
⇒ ∠(MOF) = ∠(MEH)
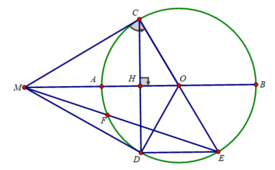
c) Ta có: ΔCOD cân tại O có OH là đường cao cũng là đường trung tuyến của tam giác
⇒ CH = HD = CD/2 ⇒ C H 2 = D H 2 = C D 2 / 4
Tam giác ACH vuông tại H có:
A H 2 + C H 2 = C A 2 ⇒ A H 2 + C D 2 / 4 = C A 2 (1)
Tam giác CHB vuông tại H có:
B H 2 + C H 2 = C B 2 ⇒ B H 2 + C D 2 / 4 = C B 2 (2)
Từ (1) và (2) ta có:
a: Xét ΔOCD có
OM vừa là đường cao, vừa là trung tuyến
Do đó: ΔOCD cân tại O
mà OM là đường cao
nên OM là phân giác của góc COD
b: Xét ΔOCM và ΔODM có
OC=OD
góc COM=góc DOM
OM chung
Do đó: ΔOCM=ΔODM
=>góc ODM=góc OCM=90 độ
=>MD là tiếp tuyến của (O)
c: Xét ΔDMO vuông tại D có DH là đường cao
nên MH*MO=MD^2
Xét ΔOCM vuông tại C có CH là đường cao
nên OH*OM=OC^2
=>4*OH*OM=4*OC^2=MA^2
