Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔOCD cân tại O
mà OM là đường cao
nen OM là phân giác của góc COD và I là trung điểm của CD
Xét ΔOCM và ΔODM có
OC=OD
góc COM=góc DOM
OM chung
Do đó: ΔOCM=ΔODM
=>góc ODM=90 độ
=>MD là tiếp tuyến của (O)
b: Xét ΔMCB và ΔMAC có
góc MCB=góc MAC
góc CMB chung
DO đó: ΔMCB đồng dạng với ΔMAC
=>MC/MA=MB/MC
=>MC^2=MB*MA=MI*MO

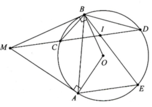
a, Vì M B C ^ = M D B ^ = 1 2 s đ C B ⏜ nên chứng minh được ∆MBC:∆MDB (g.g)
b, Vì
M
B
O
^
+
M
A
O
^
=
180
0
nên tứ giác MAOB nội tiếp
c, Đường tròn đường kính OM là đường tròn ngoại tiếp tứ giác MAOB => r = M O 2
Gọi H là giao điểm của AB với OM
=> OH ⊥ AB; AH = BH = R 3 2
Giải tam giác vuông OAM, đường cao AH ta được OM = 2R Þ r = R
d, Ta có M I B ^ = s đ D E ⏜ + s đ B C ⏜ 2 và M A B ^ = s đ A C ⏜ + s đ B C ⏜ 2
Vì AE song song CD => s đ D E ⏜ = s đ A C ⏜ => M I B ^ = M A B ^
Do tứ giác MAIB nội tiếp hay 5 điểm A, B, O, I, M nằm trên cùng 1 đường tròn kính MO
Từ đó ta có được M I O ^ = 90 0 => OI ⊥ CD hay I là trung điểm của CD

a. Do I là trung điểm dây cung BC nên ta có \(\widehat{OIC}=90^0\). Xét tứ giác MOCI có \(\widehat{CMO}+\widehat{CIO} =90^0+90^0=180^0\) nên tứ giác MOIC là tứ giác nội tiếp đường tròn đường kính CO.
b. Do D là điểm chính giữa cung AB nên \(DO \perp AB\), mà \(CM \perp AB\) nên \(DO \parallel CM\). Từ đó dễ thấy \(dtCMD=dtCMO\).
\(\frac{1}{2}CM.MO\le\frac{1}{2}\frac{CM^2+OM^2}{2}=\frac{1}{4}OC^2=\frac{R^2}{4}\)
Vậy diện tích tam giác MCD lớn nhất bằng \(\frac{R^2}{4}\) khi \(OM=\frac{R}{\sqrt{2}}\)
Chúc em học tốt ^^