Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

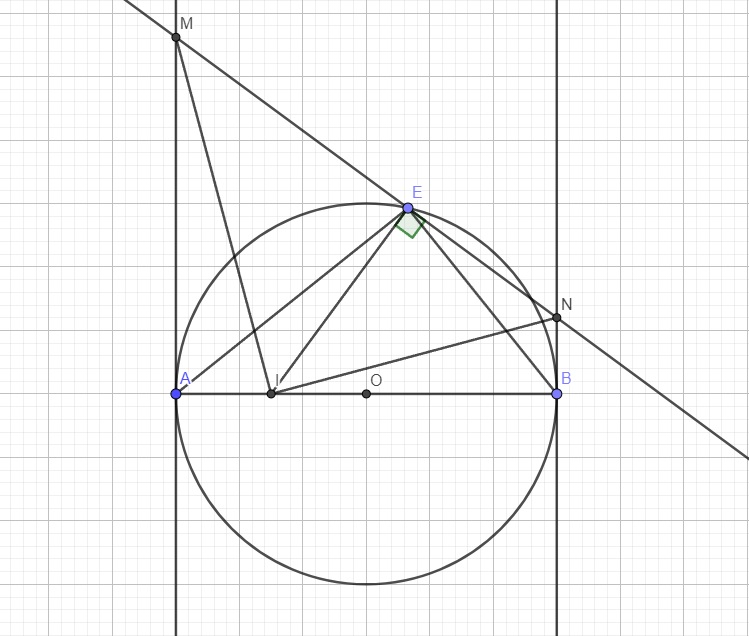
1: góc MAI+góc MEI=180 độ
=>MAIE nội tiếp
2: góc IEN+góc IBN=180 độ
=>IENB nội tiếp
MAIE nội tiếp
=>góc AMI=góc AEI
IENB nội tiếp
=>góc BIN=góc BEN
góc BEN+góc IEB=90 độ
góc AEI+góc BEI=90 độ
=>góc BEN=góc AEI
=>góc AMI=góc BIN

a. Em tự giải
b.
Do \(AM||BN\) (cùng vuông góc AB) \(\Rightarrow\widehat{AMN}+\widehat{BNM}=180^0\) (2 góc trong cùng phía)
Mà \(\widehat{AMN}+\widehat{AIE}=180^0\) (AMEI nội tiếp) \(\Rightarrow\widehat{AIE}=\widehat{BNM}\) (1)
Lại có \(\widehat{NBE}=\widehat{BAE}\) (cùng phụ \(\widehat{ABE}\)) (2)
(1);(2) \(\Rightarrow\Delta IAE\sim\Delta NBE\left(g.g\right)\) (3)
\(\Rightarrow\dfrac{IE}{NE}=\dfrac{IA}{NB}\Rightarrow IA.NE=IE.NB\)
\(\Rightarrow\dfrac{1}{3}IB.NE=IE.NB\Rightarrow IB.NE=3IE.NB\)
c.
AMEI nội tiếp \(\Rightarrow\widehat{AMI}=\widehat{AEI}\) (cùng chắn AI)
Từ (3) \(\Rightarrow\widehat{AEI}=\widehat{NEB}\) \(\Rightarrow\widehat{AMI}=\widehat{NEB}\)
Lại có tứ giác BNEI nội tiếp (B và E đều nhìn IN dưới 1 góc vuông)
\(\Rightarrow\widehat{NEB}=\widehat{NIB}\) (cùng chắn NB)
\(\Rightarrow\widehat{AMI}=\widehat{NIB}\)
\(\Rightarrow\Delta_VAMI\sim\Delta_VBIN\left(g.g\right)\)
\(\Rightarrow\dfrac{AM}{BI}=\dfrac{AI}{BN}\Rightarrow AM.BN=AI.BI=\dfrac{R}{2}.\dfrac{3R}{2}=\dfrac{3R^2}{4}\)
Đặt \(AM=x>0\Rightarrow BN=\dfrac{3R^2}{4x}\)
Ta có: \(S_{MIN}=S_{ABNM}-\left(S_{AMI}+S_{BIN}\right)=\dfrac{\left(AM+BN\right).AB}{2}-\left(\dfrac{AM.AI}{2}+\dfrac{BN.BI}{2}\right)\)
\(=\dfrac{\left(x+\dfrac{3R^2}{4x}\right).2R}{2}-\left(\dfrac{x.\dfrac{R}{2}}{2}+\dfrac{\dfrac{3R^2}{4x}.\dfrac{3R}{2}}{2}\right)\)
\(=\dfrac{3Rx}{4}+\dfrac{3R^3}{16x}=\dfrac{3R}{4}\left(x+\dfrac{R^2}{4x}\right)\ge\dfrac{3R}{4}.2\sqrt{\dfrac{R^2x}{4x}}=\dfrac{3R^2}{4}\)
Dấu "=" xảy ra khi \(x=\dfrac{R}{2}\) hay \(AM=AI\)

a/
\(d_1;d_2\) là tiếp tuyến với đường tròn tại A và B \(\Rightarrow d_1\perp AB;d_2\perp AB\) => \(d_1\)//\(d_2\)
Xét tg vuông ABK có
\(\widehat{ACB}=90^o\) (góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow AK^2=KC.KB\) (Trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu của cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
b/
Ta có
DA=DC (2 tiếp tuyến của 1 đường tròn cùng xuất phát từ 1 điểm thì khoảng cách từ điểm đó đến 2 tiếp điểm bằng nhau) (1)
EC=EB (lý do như trên) => tg EBC cân tại E\(\Rightarrow\widehat{ECB}=\widehat{KBE}\) (2 góc ở đáy của tg cân) (*)
\(\widehat{KBE}=\widehat{AKB}\) (góc so le trong) (**)
\(\widehat{KCD}=\widehat{ECB}\) (Góc đối đỉnh) (***)
Từ (*) (**) và (***) \(\Rightarrow\widehat{AKB}=\widehat{KCD}\) => tg DCK cân tại D => DC=DK (2)
Từ (1) và (2) => DA=DK nên K là trung điểm của AK
c/ Gọi I là giao của CH với BD
Ta có
\(CH\perp AB;d_1\perp AB\) => CH//\(d_1\)
\(\Rightarrow\frac{IC}{DK}=\frac{BC}{BK}=\frac{BH}{BA}=\frac{IH}{DA}\) (Talet trong tam giác)
Mà DK=DA => IC=IH => BD đi qua trung điểm I của CH
d/
câu a ý số 2 bạn còn cách nào khác ko? Tại mk chx hc góc nội tiếp chắn nửa đường tròn

a: góc MAI+góc MEI=180 độ
=>MAIE nội tiếp
b: góc NEI+góc NBI=180 độ
=>NEIB nội tiếp
=>góc ENI=góc EBI
góc MIN=góc MIE+góc NIE
=góc MAE+góc NBE
=90 độ-góc EAI+90 độ-góc EBI
=90 độ

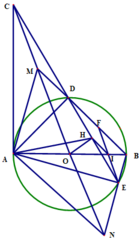
a) Ta có
C A B ⏜ = 90 0 O H C ⏜ = 90 0 ⇒ C A B ⏜ + O H C ⏜ = 180 0
Vậy tứ giác AOHC nội tiếp.
b) Ta có C A D ⏜ = A E C ⏜ , A C E ⏜ chung suy ra Δ A C D ~ Δ E C A (g.g)
⇒ C A C E = A D A E ⇒ A C . A E = A D . C E
c) Từ E vẽ đường thẳng song song với MN cắt cạnh AB tại I và cắt cạnh BD tại F ⇒ H E I ⏜ = H C O ⏜ .
Vì tứ giác AOHC nội tiếp ⇒ H A O ⏜ = H C O ⏜ = H E I ⏜ .
Suy ra tứ giác AHIE nội tiếp ⇒ I H E ⏜ = I A E ⏜ = B D E ⏜ ⇒ H I / / B D .
Mà H là trung điểm của DE=> I là trung điểm của EF. Có EF//MN và IE= IF
=> O là trung điểm của đoạn thẳng MN.
Suy ra tứ giác AMBN là hình bình hành => AM//BN.