Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔOBC cân tại O
mà OH là đường cao
nên H là trung điểm của BC
=>HB=HC=24/2=12cm
ΔOHB vuông tại H
=>\(OH^2+HB^2=OB^2\)
=>\(OH^2+12^2=15^2\)
=>\(OH^2=15^2-12^2=81\)
=>OH=9(cm)
b: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
ΔOBC cân tại O
mà OH là đường trung tuyến
nên OH là đường trung trực của BC(2)
Từ (1),(2) suy ra O,H,A thẳng hàng
c:Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2\)
=>\(OA=\dfrac{OB^2}{OH}=\dfrac{15^2}{9}=25\left(cm\right)\)
ΔOBA vuông tại B
=>\(OB^2+BA^2=OA^2\)
=>\(BA^2+15^2=25^2\)
=>\(BA^2=625-225=400\)
=>BA=20(cm)
AB=AC
mà AB=20cm
nên AC=20cm
d: Xét ΔOBM vuông tại B và ΔOCN vuông tại C có
OB=OC
\(\widehat{BOM}=\widehat{CON}\)
Do đó: ΔOBM=ΔOCN
=>BM=CN
Xét ΔAMN có \(\dfrac{AB}{BM}=\dfrac{AC}{CN}\)
nên BC//MN
AB+BM=AM
AC+CN=AN
mà AB=AC và BM=CN
nên AM=AN
=>\(\widehat{BMN}=\widehat{CNM}\)
Xét tứ giác BCNM có BC//MN
nên BCNM là hình thang
Hình thang BCNM có \(\widehat{BMN}=\widehat{CNM}\)
nen BCNM là hình thang cân

a) Dùng Pytago ta tính được OH=9cm
b) Vì và nên OA là đường trung trực BC
Mà H là trung điểm BC
=>A,H,O thẳng hàng.
c.\(\Delta ABO\) Vuông tại B đươngg cao BH
\(\Rightarrow\frac{1}{AB^2}=\frac{1}{BH^2}-\frac{1}{OB^2}\)
\(\Rightarrow\frac{1}{12^2}-\frac{1}{15^2}=\frac{1}{400}\)
\(\Rightarrow AB=20cm\)

a: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
mà OB=OC
nên OA là đường trung trực của BC
=>OA\(\perp\)BC tại trung điểm của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2\)
=>\(OH\cdot6=3^2=9\)
=>OH=1,5(cm)
b: Xét ΔOBA vuông tại B có \(cosBOA=\dfrac{OB}{OA}=\dfrac{1}{2}\)
nên \(\widehat{BOA}=60^0\)
Xét ΔOBI có OB=OI và \(\widehat{BOI}=60^0\)
nên ΔOBI đều
ΔOBI đều
mà BH là đường cao
nên H là trung điểm của OI
Xét tứ giác OBIC có
H là trung điểm chung của OI và BC
nên OBIC là hình bình hành
Hình bình hành OBIC có OB=OC
nên OBIC là hình thoi
ΔOBA vuông tại B
=>\(\widehat{BOA}+\widehat{BAO}=90^0\)
=>\(\widehat{BAO}+60^0=90^0\)
=>\(\widehat{BAO}=30^0\)
Xét ΔABC có AB=AC
nên ΔABC cân tại A
ΔABC cân tại A
mà AH là đường cao
nên AH là phân giác của \(\widehat{BAC}\)
=>\(\widehat{BAC}=2\cdot\widehat{BAH}=60^0\)
=>ΔBAC đều
c: Xét (O) có
DB,DM là tiếp tuyến
Do đó: DB=DM
Xét (O) có
EM,EC là tiếp tuyến
=>EM=EC
DE=DM+ME
mà DM=DB và CE=EM
nên DE=DB+EC
ΔOBA vuông tại B
=>\(BO^2+BA^2=OA^2\)
=>\(BA^2=6^2-3^2=27\)
=>\(BA=3\sqrt{3}\left(cm\right)\)
\(C_{ADE}=AD+DE+AE\)
\(=AD+AE+DB+EC\)
=AB+AC
\(=3\sqrt{3}\cdot2=6\sqrt{3}\left(cm\right)\)

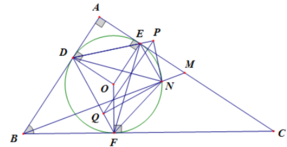
Vì DPN+DQN=90o+90o=180o nên DPNQ là tứ giác nội tiếp
=>QPN=QDN (hai góc nội tiếp cùng chắn cung QN) (5)
Mặt khác DENF là tứ giác nội tiếp nên QDN=FEN (6)
Từ (5) và (6) ta có FEN=QPN (7)
Tương tự ta có: EFN=PQN (8)
Từ (7) và (8) suy ra Δ N P Q ~ Δ N E F ( g . g ) = > P Q E F = N Q N F
Theo quan hệ đường vuông góc – đường xiên, ta có
N Q ≤ N F = > P Q E F = N Q N F ≤ 1 = > P Q ≤ E F
Dấu bằng xảy ra khi Q ≡ F ⇔ NF ⊥ DF ⇔ D, O, N thẳng hàng.
Do đó PQ max khi M là giao điểm của AC và BN, với N là điểm đối xứng với D qua O.
Tự vẽ hình
a) theo t/c 2 tiếp tuyến cắt nhau
=> AB =AC
mà OB =OC =R
=> OA là trung trực của BC => OA vuông góc BC tại H => H là trung điểm của BC => BH =BC/2 =15
Áp dụng Pi - ta -go cho HBO vuông tại H => OH2 = OB2 - BH2 = 172 - 152 =64 => OH =8
b) theo câu a => O;H;A thẳng hàng rồi
c)