Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Gọi điểm cố định đó là \(N\left(x_0;y_0\right)\) .
Vì (d) đi qua N nên : \(\left(m-2\right)x_0+\left(m-1\right)y_0-1=0\Leftrightarrow m\left(x_0+y_0\right)-\left(2x_0+y_0+1\right)=0\)
Để (d) luôn đi qua N với mọi m thì \(\begin{cases}x_0+y_0=0\\2x_0+y_0+1=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x_0=-1\\y_0=1\end{cases}\) . Vậy điểm cố định đó là N(-1;1)
b/ Gọi \(A\left(\frac{1}{m-2};0\right)\) và \(B\left(0;\frac{1}{m-1}\right)\) là hai điểm thuộc (d)
và A,B lần lượt nằm trên Ox và Oy
Khi đó \(\frac{1}{h^2}=\frac{1}{OA^2}+\frac{1}{OB^2}\)
hay \(\frac{1}{h^2}=\frac{1}{\left(m-1\right)^2}+\frac{1}{\left(m-2\right)^2}\)
Tới đây bạn tìm GTNN của \(\frac{1}{h^2}\) rồi suy ra GTLN của \(h\) nhé :)

Đáp án A
Ta có: ![]()
AM → (3; 2; 4)
Mặt phẳng (P) có vecto pháp tuyến là n p → (1; 1; 1)
Gọi H là hình chiếu vuông góc của A trên d. Ta có: d(A; d) = AH ≤ AM = 29
Dấu bằng xảy ra khi và chỉ khi H trùng M, nghĩa là d vuông góc với AM.
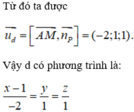

a) Thay x=-1 và y=4 vào (d), ta được:
\(3m\cdot\left(-1\right)+m-2=4\)
\(\Leftrightarrow-2m=6\)
hay m=-3
b) Để (d)//(Δ) thì \(\left\{{}\begin{matrix}3m=6\\m-2\ne-1\end{matrix}\right.\Leftrightarrow m=2\)

a: A(1;2); B(2;1)
=>\(\overrightarrow{AB}=\left(1;-1\right)\)
=>VTPT là (1;1)
Phương trình đường thẳng AB là:
1(x-1)+2(y-1)=0
=>x-1+2y-2=0
=>x+2y-3=0
b:
M(1;3); Δ: 3x+4y+10=0
Khoảng cách từ M đến Δ là:
\(d\left(M;\text{Δ}\right)=\dfrac{\left|1\cdot3+3\cdot4+10\right|}{\sqrt{3^2+4^2}}=\dfrac{\left|3+12+10\right|}{5}=5\)

a: Vì (d1)//(d) nên (d1): y=x+b
Thay x=0 và y=0 vào (d1), ta được:
b+0=0
=>b=0
b: Thay x=1 và y=4vào y=ax+6, ta được:
a+6=4
=>a=-2