Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: MN // AB (gt). \(\Rightarrow\left\{{}\begin{matrix}\widehat{MAB}=\widehat{ABC}\\\widehat{NAC}=\widehat{ACB}\end{matrix}\right.\) (so le trong).
Mà \(\widehat{ABC}=\widehat{ACB}\) (Tam giác ABC cân).
\(\Rightarrow\widehat{MAB}=\widehat{NAC.}\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (A là trung điểm của MN).
+ AB = AC (gt).
+ \(\widehat{MAB}=\widehat{NAC}\left(cmt\right).\)
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
Xét tứ giác MNCB có: \(\text{MN // CB}\) (gt).
\(\Rightarrow\) Tứ giác MNCB là hình thang.
Mà \(\widehat{M}=\widehat{N}\) (Tam giác AMB = Tam giác ANC).
\(\Rightarrow\) Tứ giác MNCB là hình thang cân.

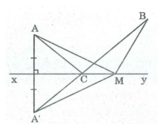
Vì A' đối xứng với A qua xy
⇒ xy là đường trung trực của AA'.
⇒ CA' = CA (t/chất đường trung trực)
MA' = MA (t/chất đường trung trực)
AC + CB = A'C + CB = A'B (1)
MA + MB = MA'+ MB (2)
Trong ∆ MA'B, ta có:
A'B < A'M + MB (bất đẳng thức tam giác) (3)
Từ (1), (2) và (3) suy ra: AC + CB < AM + MB

Cho tam giác ABC cân tại A. Trên đường thẳng đi qua đỉnh A song song với BC lấy hai điểm M và N sao cho A là trung điểm của MN (M và B cùng thuộc nửa mặt phẳng bờ là AC). Gọi H, I, K lần lượt là trung điểm MB, BC, CN. a) Chứng minh tứ giác MNCB là hình thang cân. b) Tứ giác AHIK là hình gì? Vì sao - Toán học Lớp 8 - Bài tập Toán học Lớp 8 - Giải bài tập Toán học Lớp 8 | Lazi.vn - Cộng đồng Tri thức & Giáo dục

cho mik hỏi H,I,K chỉ thuộc các cạnh đó hay là trung điểm

Gọi khoảng cách từ A,B,C đến d theo thứ tự là D,E,F
Ta có \(AD//BE\left(\perp d\right)\) nên ABED là hình thang
Mà \(AC=CB;AD//BE//CF\left(\perp d\right)\) nên \(DF=FE\)
Do đó CE là đường trung bình hình thang ABED
\(\Rightarrow CE=\dfrac{AD+BE}{2}=\dfrac{18}{2}=9\left(cm\right)\)
Vậy k/c từ C đến d là 9 cm

Hình vẽ hơi xấu trìn hbafy nhớ vẽ đẹp =)
Gọi H,I,K lần lượt là các chân cao đường cao của A,C,B đường thẳng d,AH = 12cm BK= 16cm
=> CI là khoản cách từ C đến đường thẳng d
Ta thấy ABKH là hình thang nằm nghiêng (có thể quan sát hình) (đáy AH và BK) là đường trung bình CI
Từ đó \(\frac{\left(AH+BK\right)}{2}=\frac{\left(12+16\right)}{2}=14cm\)
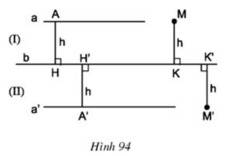
Góc AHH’ = góc HH’A’ (= 90o). Mà 2 góc đó là 2 góc so le trong
⇒ a // b
Và a // a’
⇒ a’ // b
- Tứ giác AMKH có AH = MK (= h) và AH // MK (cùng ⊥ b)
⇒ Tứ giác AMKH là hình bình hành ⇒ AM // HK
Mà a // b ⇒ a // HK
Do đó AM trùng với a hay M ∈ a
- Chứng minh tương tự: M’ ∈ a’