Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

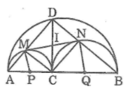
Gọi O là trung điểm của AB
Tứ giác CMDN là hình chữ nhật nên CD = MN
Trong tam giác OCD ta có: CD ≤ OD nên MN ≤ OD
Vì OD không đổi nên MN = OD là giá trị lớn nhất khi và chỉ khi C trùng với O
Vậy C là trung điểm của AB thì MN có độ dài lớn nhất.

a/ Ta có : \(\hept{\begin{cases}AH\text{//}OM\text{//}BK\\OA=OB\end{cases}}\) \(\Rightarrow\)OM là đường trung bình của hình thang ABKH
\(\Rightarrow\)\(AH+BK=2OM=2R\) (không đổi)
b/ Từ M hạ MN vuông góc với AB tại N (1)
Ta sẽ chứng minh MN = MK
Xét trong (O;R) thì : \(\widehat{BMK}=\widehat{MAB}\) (cùng chắn cung MB)
Mà : \(\hept{\begin{cases}\widehat{BMK}+\widehat{MBK}=90^o\\\widehat{MAB}+\widehat{MBA}=90^o\end{cases}}\) \(\Rightarrow\)\(\widehat{MBA}=\widehat{MBK}\)
Xét hai tam giác vuông NBM và KBM có MB là cạnh huyền (chung) , \(\widehat{MBA}=\widehat{MBK}\)
\(\Rightarrow\)\(\Delta NBM=\Delta KBM\) (ch.gn)
\(\Rightarrow\) MN = MK (2)
Từ (1) và (2) suy ra đpcm.
c/ Vì ABKH là hình thang vuông nên \(S_{ABKH}=\frac{1}{2}\left(AH+BK\right).HK=\frac{1}{2}.2OM.HK\)
\(=\left(2MN\right).OM\) . Mà OM = R không đổi, vậy \(maxS_{ABKH}\Leftrightarrow maxMN\Leftrightarrow MN=OM\)\(\Leftrightarrow\)M là điểm chính giữa cung AB
Khi đó thì : \(S_{ABKH}=2OM.OM=2R^2\)

