Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tương tự bài 4. kéo dài AC và BD cắt nhau tại E. Từ đó chứng minh được I thuộc đường trung bình của DABE.

+ Từ I kẻ đường thẳng //AC cắt AB tại K; Từ I kẻ đường thẳng //BD cắt AB tại H
+ Ta sẽ c/m được tam giác IKH là tam giác đều
+ Ta cũng sẽ c/m được AK=MK; MH=BH
=> MK=AM/2 và MH=BM/2 => KH=MK+MH=(AM+BM)/2=AB/2
=> tam giác IKH là tam giác đều có độ dài các cạnh không thay đổi => đường cao hạ từ I xuống AB cắt AB tại F và IF không thay đổi
=> I chạy trên đường thẳng //AB có độ dài \(IF=\sqrt{IA^2-AF^2}=\sqrt{\left(\frac{AB}{2}\right)^2-\left(\frac{AB}{4}\right)^2}=\sqrt{3}.\frac{AB}{4}\)

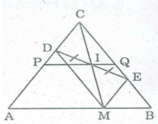
Gọi C là giao điểm của AD và BE.
Tam giác ABC có:
∠ A = 60 0 (vì ΔADM đều)
∠ B = 60 0 ( vì ΔBEM đều)
Nên ∠ C = 180 0 - ∠ A - ∠ B = 60 0
Suy ra: ∆ ABC đều hay AB = AC = BC
Suy ra điểm C cố định.
Lại có: ∠ A = ∠ (EMB ) = 60 0
ME // AC ( vì có cặp góc đồng vị bằng nhau)
Hay ME // CD.
Do ∠ DMA = ∠ BEM = 60 0 ( hai tam giác AMD và BME là tam giác đều )
Suy ra: MD // BC ( vì có cặp góc so le trong bằng nhau ).
hay MD // EC
suy ra tứ giác CDME là hình bình hành.
I là trung điểm của DE nên I là trung điểm của CM
Kẻ CH ⊥ AB,IK ⊥ AB⇒IK // CH
Trong ∆ CHM,ta có:CI = IM và IK // CH
Suy ra IK là đường trung bình của ΔCHM⇒IK = 1/2 CH
Vì C cố định nên CH không đổi ⇒ IK = 1/2 CH không đổi nên I chuyển động trên đường thẳng song song với AB, cách AB một khoảng bằng 1/2 CH
Khi M trùng với A thì I trùng với trung điểm P của AC.
Khi M trùng với B thì I trùng với trung điểm Q của BC.
Vậy khi M chuyển động trên đoạn thẳng AB thì I chuyển động trên đoạn PQ ( P là trung điểm AC, Q là trung điểm BC).
Tương tự 2B. Gợi ý: Kéo dài AC và BD cắt nhau tại E. Xét các trường hợp khi M º A Þ C º A, D º E và khi M º B Þ D º B, C º E.
Từ đó chứng minh được I thuộc đường trung bình của DABE.