Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Vì AE là vừa là đg cao (AE⊥HM) vừa là trung tuyến nên tg AHM cân tại A
Do đó AH=AM
Vì AF là vừa là đg cao (AF⊥HN) vừa là trung tuyến nên tg AHN cân tại A
Do đó AH=AN
Từ đó ta được AM=AN hay tg AMN cân tại A
b, Vì E,F là trung điểm HM,HN nên EF là đtb tg MHN
Do đó EF//MN
c, Vì AI là trung tuyến tg AMN cân tại A nên AI cũng là đg cao
Do đó AI⊥MN
Mà EF//MN nên AI⊥EF
d, Vì tg AEH và tg AFH cân tại A nên AE,AF lần lượt là p/g \(\widehat{MAH}\) và \(\widehat{NAH}\)
Do đó \(\widehat{MAN}=\widehat{MAH}+\widehat{NAH}=2\cdot\widehat{EAH}+2\cdot\widehat{FAH}=2\cdot\widehat{BAC}\)

a/ Ta có : AE là cạnh chung của hai tam giác vuông: tam giác AME và tam giác AHE ; ME = EM (gt)
=> tam giác AME = tam giác AHE (2 cạnh góc vuông)
b/ Dễ thấy EH = EM ; AB vuông góc MH => đpcm
Tương tự với AC .
c/ Ta chứng minh được : AB là đường trung trực của MH
=> AM = AH (1)
AC là đường trung trực của NH => AH = AN (2)
Từ (1) và (2) suy ra AM = AN => tam giác AMN cân tại A
d/ Hãy chứng minh MN // EF

Em tham khảo bài dưới đây:
Câu hỏi của ngô thị gia linh - Toán lớp 8 - Học toán với OnlineMath
a) \(\Delta AME=\Delta AHE\) (Hai cạnh góc vuông)

a) Do EM = EH và AE vuông góc MH tại E nên AB là đường trung trực của MH. Tương tự AC là trung trực HN.
b) Do AB là đường trung trực của MH nên AM = AH. Tương tự AH = AN
Vậy AM = AN hay tam giác AMN cân tại A.
c) Xét tam giác HMN có E, F lần lượt là trung điểm HM, HN nên EF là đường trung bình tam giác.
Vậy EF // MN.
d) Tam giác cân AMN có I là trung điểm MN nên \(AI⊥MN\)
Lại có MN //EF nên \(AI⊥EF.\)

a) Ta thấy AB vuông góc với MH tại trung điểm E của MH nên AB là đường trung trực của MH.
Ta thấy AC vuông góc với NH tại trung điểm F của NH nên AC là đường trung trực của NH.
b) Do AB là trung trực của MH nên AM = AH.
Tương tự AN = AH. Vậy nên AM = AN hay tam giác AMN cân tại A.
c) Xét tam giác HMN có E là trung điểm MH, F là trung điểm HN nên EF là đường trung bình tam giác HMN.
Suy ra EF // MN.
d) Do tam giác AMN cân tại A nên trung tuyến AI đồng thời là đường cao. Vậy AI vuông góc MN.
Lại có MN // EF nên AI vuông góc EF.

+ A,B thuộc đg trung trực của HM
\(\Rightarrow\left\{{}\begin{matrix}AM=AH\\BM=BH\end{matrix}\right.\)
+ ΔABH = ΔABM ( c.c.c )
\(\Rightarrow\left\{{}\begin{matrix}\widehat{AMB}=\widehat{AHB}=90^o\Rightarrow BM\perp AM\\AM=AH\end{matrix}\right.\)
+ Tương tự ta cm đc: AN = AH
=> AM = AN => ΔAMN cân tại A
=> Đg trung tuyến AI của ΔAMN cx đồng thời là đg cao
=> AI ⊥ EF

a: Xét tứ giác AEHF có
góc AEH=góc AFH=góc FAE=90 độ
nên AEHF là hình chữ nhật
=>EF=AH
b: \(S_{ABC}=\dfrac{1}{2}\cdot3\cdot4=2\cdot3=6\left(cm^2\right)\)
\(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
AH=3*4/5=2,4cm

Gọi P là giao của BN với EH; Q là giao của MN với HF; K là giao của MN với EF
Ta có
\(EH\perp BC;AI\perp BC\)=> EH//AI \(\Rightarrow\frac{PE}{NA}=\frac{PH}{NI}\) (Talet) \(\Rightarrow\frac{PE}{PH}=\frac{NA}{NI}=1\Rightarrow PE=PH\)
=> BN đi qua trung điểm P của EH
Ta có
EF//BC (gt) => KF//HM \(\Rightarrow\frac{QK}{QM}=\frac{QF}{QH}=\frac{KF}{HM}\) (Talet) => KH//FM
Xét tứ giác KFMH có
KF//HM; KH//FM => KFMH là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
=> KF=HM (Trong hình bình hành các cạnh đối bằng nhau)
\(\Rightarrow\frac{QF}{QH}=\frac{KF}{HM}=1\Rightarrow QF=QH\)
=> MN đi qua trung điểm Q của HF
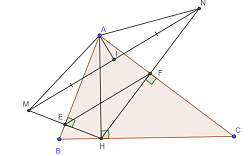
Lời giải:
a. Xét tam giác $AME$ và $AHE$ có:
$AE$ chung
$\widehat{AEM}=\widehat{AEH}=90^0$
$ME=HE$ (gt)
$\Rightarrow \triangle AME=\triangle AHE$(c.g.c)
$\Rightarrow AM=AH(1)$
Hoàn toàn tương tự ta có $\triangle AHF=\triangle ANF$ (c.g.c)
$\Rightarrow AH=AN(2)$
Từ $(1); (2)\Rightarrow AM=AN$ nên tam giác $AMN$ là tam giác cân tại $A$.
b.
Ta có:
$\frac{HE}{EM}=\frac{HF}{FN}=1$ nên theo định lý Talet thì $EF\parallel MN$
c.
Vì tam giác $AMN$ cân tại $A$ (cm ở phần a) nên trung tuyến $AI$ đồng thời là đường cao.
$\Rightarrow AI\perp MN$
Mà $MN\parallel EF$
$\Rightarrow AI\perp EF$ (đpcm)
Hình vẽ: