
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


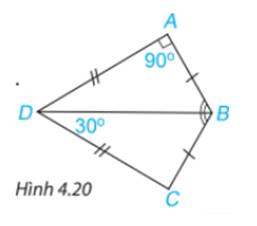
a) Xét \(\Delta ABD\) và \(\Delta CBD\)có:
DA=DC(gt)
BD chung
BA=BC
Vậy \(\Delta ABD = \Delta CBD\)(c.c.c)
b) Ta có \(\widehat A = \widehat C = {90^o}\)(hai góc tương ứng)
Theo định lí tổng ba góc trong tam giác BCD, ta có:
\(\begin{array}{l}\widehat C + \widehat {CDB} + \widehat {DBC} = {180^o}\\ \Rightarrow {90^o} + {30^o} + \widehat {DBC} = {180^o}\\ \Rightarrow \widehat {DBC} = {60^o}\end{array}\)
Mà \(\Delta ABD = \Delta CBD\) nên \(\widehat {ABD} = \widehat {CBD}\) ( 2 góc tương ứng)
\(\Rightarrow \widehat {ABD} = \widehat {CBD} = {60^o}\\\Rightarrow \widehat {ABC} = \widehat {ABD} + \widehat {CBD} = {60^o} + {60^o} = {120^o}\)

\(1,\widehat{A}+\widehat{B}+\widehat{C}=180^0\\ \text{Mà }\widehat{A}=\widehat{B}=\widehat{C}\\ \Rightarrow\widehat{A}=\widehat{B}=\widehat{C}=\dfrac{180^0}{3}=60^0\\ 2,\widehat{A}+\widehat{B}+\widehat{C}=180^0\\ \Rightarrow\widehat{B}+\widehat{C}=180^0-\widehat{A}=110^0\\ \text{Mà }\widehat{B}-\widehat{C}=10^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{B}=\left(110^0+10^0\right):2=60^0\\\widehat{C}=60^0-10^0=50^0\end{matrix}\right.\)

Xét tam giác vuông ABC và tam giác vuông ADE có :
AB=AD
AC=AE
=> tam giác ABC= tam giác ADE ( 2 cạnh góc vuông )

Ta có tg ABC vuông( A= 90độ)
lại có B= 30 độ
Suy ra: tg ABC là nửa tg đều
Suy ra:AB=1/2BC
Suy ra:BC=2AB=2*3=6cm
Ta có AC= Căn BC-Căn AB=2cm
Ta có \(\widehat{A}=90^o;\widehat{B}=30^o\Rightarrow\widehat{C}=180^o\left(\widehat{A}+\widehat{B}\right)=180^o+\left(90^o+30^o\right)\)
\(\Rightarrow\widehat{C}=180^o-120^o=60^o\)
Ta thấy góc C đối diện cạnh AB,góc A đối.....,Góc B....
Góc A = Góc B x 3=Góc C x2
\(\Rightarrow AC=\frac{BC}{2}\)
\(\Rightarrow2.AC=BC\)
Áp dụng Pytago vào tam giác
\(AB^2=BC^2-AC^2\)
\(\Rightarrow3^2=\left(2AC\right)^2-AC^2\)
\(\Rightarrow9=4.AC^2-AC^2\)
\(\Rightarrow3.AC^2\)
\(\Rightarrow AC^2=3\)
\(\Rightarrow AC=\sqrt{3}\)
Áp dụng Pytago vào tam giác ( tính BC)
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC^2=9+3\left(\sqrt{3^2}\right)\)
\(\Rightarrow BC^2=12\)
\(\Rightarrow BC=\sqrt{12}\)