Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

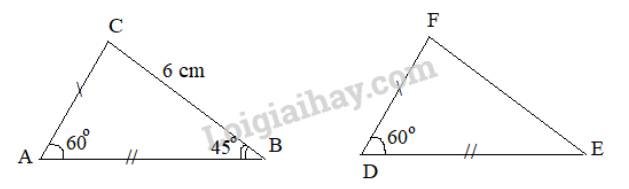
Xét hai tam giác ABC và DEF có:
\(\begin{array}{l}AB = DE\\AC = DF\\\widehat {BAC} = \widehat {EDF} (= {60^\circ })\end{array}\)
\(\Rightarrow \Delta ABC = \Delta DEF\)(c.g.c)
Do đó:
\(BC=EF = 6cm\) ( 2 cạnh tương ứng)
\( \widehat {ABC} =\widehat {DEF}= {45^o}\) (2 góc tương ứng)
\(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = {180^o}\\ \Rightarrow {60^o} + {45^o} + \widehat {ACB} = {180^o}\\ \Rightarrow \widehat {ACB} = {75^o}\end{array}\)
\( \Rightarrow \widehat {EFD} = \widehat {ACB} = {75^o}\)

a)
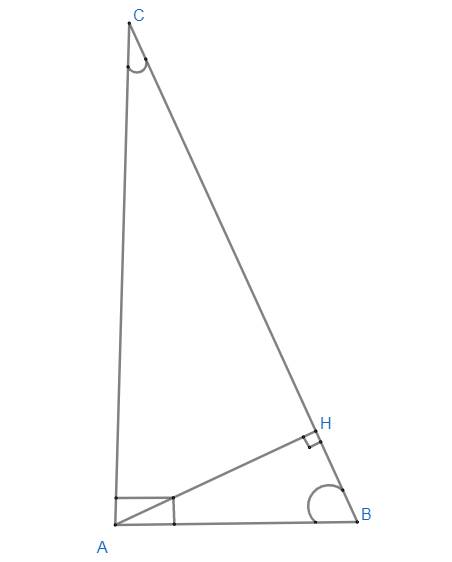
Xét 2 tam giác vuông ABC và HAC có:
\(\widehat{C}\) chung
=> tg ABC \(\sim\) td HAC (g.g)
=> \(\widehat{ABC}=\widehat{HAC}\)
b)
Xét 2 tg vuông ACB và HAB có:
\(\widehat{B}\) chung
=> tg ACB \(\sim\) tg HAB (g.g)
=> \(\widehat{ACB}=\widehat{HAB}\)

trần hà my
Nguyễn Huy Tú
Nguyễn Huy Thắng
Akai Haruma
Help me !!!!!!!!!!!!!!!!

Ta có tg ABC vuông( A= 90độ)
lại có B= 30 độ
Suy ra: tg ABC là nửa tg đều
Suy ra:AB=1/2BC
Suy ra:BC=2AB=2*3=6cm
Ta có AC= Căn BC-Căn AB=2cm
Ta có \(\widehat{A}=90^o;\widehat{B}=30^o\Rightarrow\widehat{C}=180^o\left(\widehat{A}+\widehat{B}\right)=180^o+\left(90^o+30^o\right)\)
\(\Rightarrow\widehat{C}=180^o-120^o=60^o\)
Ta thấy góc C đối diện cạnh AB,góc A đối.....,Góc B....
Góc A = Góc B x 3=Góc C x2
\(\Rightarrow AC=\frac{BC}{2}\)
\(\Rightarrow2.AC=BC\)
Áp dụng Pytago vào tam giác
\(AB^2=BC^2-AC^2\)
\(\Rightarrow3^2=\left(2AC\right)^2-AC^2\)
\(\Rightarrow9=4.AC^2-AC^2\)
\(\Rightarrow3.AC^2\)
\(\Rightarrow AC^2=3\)
\(\Rightarrow AC=\sqrt{3}\)
Áp dụng Pytago vào tam giác ( tính BC)
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC^2=9+3\left(\sqrt{3^2}\right)\)
\(\Rightarrow BC^2=12\)
\(\Rightarrow BC=\sqrt{12}\)

b,Gọi I là giao điểm của BC và ED
Xét ∆AED và ∆ABC có:
+AB=AD(gt)
+\(\widehat{BAC}=\widehat{DAB}\left(=90^o\right)\)
+AC=AE(gt)
\(\Rightarrow\)∆AED=∆ABC(ch-cgv)
\(\Rightarrow\widehat{EDA}=\widehat{ABC}\) (2 góc tương ứng)
Mà \(\widehat{DEA}+\widehat{EDA}=90^o\)( do ∆ADE vuông tại A)
\(\Rightarrow\widehat{CBA}+\widehat{DEA}=90^o\)
\(\Rightarrow\)∆BIE vuông tại I
\(\Rightarrow DE\perp BC\)

AB là
( 49 + 7 ) : 2 = 28
AC là
28 - 7 = 21
Xét tam giác ABC vuông tại A
AB^2 + AC^2 = BC^2
21^2 + 28^2 = BC^2
BC^2 = 1225
BC = 35

a: Xét ΔHAB vuông tại H có \(\widehat{ABH}=45^0\)
nên ΔHAB vuông cân tại H
b: \(AB=\sqrt{AH^2+HB^2}=AH\sqrt{2}\)

chọn A
A