K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
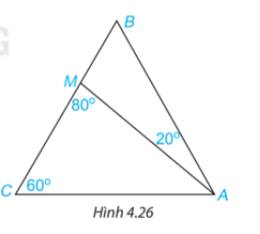
Ta có:
\(\widehat {AMB} + \widehat {AMC} = {180^o}\)( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {AMB} + {80^o} = {180^o}\\ \Rightarrow \widehat {AMB} = {100^o}\end{array}\)
Áp dụng định lí tổng ba góc trong một tam giác:
+) Trong tam giác AMB có:
\(\begin{array}{l}\widehat {ABC} + \widehat {MAB} + \widehat {AMB} = {180^O}\\ \Rightarrow \widehat {ABC} + {20^o} + {100^o} = {180^O}\\ \Rightarrow \widehat {ABC} = {60^o}\end{array}\)
+) Trong tam giác ABC có:
\(\begin{array}{l}\widehat {BAC} + \widehat {ACB} + \widehat {CBA} = {180^o}\\ \Rightarrow \widehat {BAC} + {60^o} + {60^o} = {180^o}\\ \Rightarrow \widehat {BAC} = {60^o}\end{array}\)
Trên nửa mặt phẳng bờ BC có chứa điểm A, ta dựng 1 tam giác đều BIC.
Gọi giao điểm của tia CI với AB là K.
Dễ thấy 3 điểm B,I,E thẳng hàng (Do ^CBI=^CBE=600)
Ta có: ^ABC=^ACB => ^ABE+^CBE=^ACK+^BCK. Mà ^CBE=^BCK=600
=> ^ABE=^ACK => \(\Delta\)AEB=\(\Delta\)AKC (g.c.g) = >AE=AK (2 cạnh tương ứng)
=> \(\Delta\)AKE cân tại A. Mà 2 điểm K và E lần lượt thuộc 2 cạnh AB và AC của \(\Delta\)ABC cân tại A
=> KE//BC => Dễ dàng chứng minh được \(\Delta\)KEI đều => KE=IE=IK
Xét \(\Delta\)DBC: Có ^DBC=800 và ^BCD=500.
Thấy rằng 500=(1800-800)/2 => \(\Delta\)DBC cân tại đỉnh B => BC=BD
Vì \(\Delta\)BIC đều nên BC=BI => BD=BI => \(\Delta\)DBI cân tại B
Có thể tính được ^IBD=200 => ^BDI=^BID=800
=> ^DIK=^BIK-^BID= 1200-800 = 400. (Do ^BIK=1200) (1)
Xét \(\Delta\)KBC: ^KBC=800; ^KCB=600 => ^BKC=400 hay ^DKI=400 (2)
Từ (1) và (2) => ^DIK=^DKI => \(\Delta\)KDI cân tại D => DK=DI
Xét \(\Delta\)DKE và \(\Delta\)DIE có: DK=DI; DE chung; KE=IE (cmt) => \(\Delta\)DKE=\(\Delta\)DIE (c.c.c)
=> ^KED=^IED (2 góc tương ứng). Mà ^KED+^IED=^KEI=600 => ^IED= 600/2 =300
hay ^BED=300.
ĐS:...
Mình làm được rồi nhưng thấy bảo là Toán lớp 7 nên lỡ xóa đi. Bây giờ chả nhớ cách giải. Hu Hu