OLM cung cấp gói bải giảng điện tử PPT cho giáo viên đầu năm học

Thi thử và xem hướng dẫn giải chi tiết đề tham khảo 12 môn thi Tốt nghiệp THPT 2025

Tham gia cuộc thi "Nhà giáo sáng tạo" ẫm giải thưởng với tổng giá trị lên đến 10 triệu VNĐ

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
TM
thanh mai
27 tháng 11 2023

Cho dãy số (Un) xác định bởi: {U1=2; Un+1= 2Un + 3.2^n+1;∀n ϵ N*

Tính lim Un/(2n + 1).2^n-1

Ai đó giải bài tập giúp em với ạ, em cảm ơn rất nhiều

 
#Toán lớp 11
0
PT
Pham Trong Bach
14 tháng 6 2018
Cho dãy số ( u n ) xác định bởi  u 1   =   1 u n + 1   =   2 u n   +   3 u n   +   2     v ớ i   n ≥ 1 a) Chứng minh rằng u n   >   0 với mọi n. b) Biết ( u n ) ...
Đọc tiếp

Cho dãy số ( u n ) xác định bởi  u 1   =   1 u n + 1   =   2 u n   +   3 u n   +   2     v ớ i   n ≥ 1

a) Chứng minh rằng u n   >   0 với mọi n.

 

b) Biết ( u n ) có giới hạn hữu hạn. Tìm giới hạn đó.
#Toán lớp 11
1
CM
Cao Minh Tâm
14 tháng 6 2018

Đúng(0)
PT
Pham Trong Bach
14 tháng 3 2019
Cho dãy số ( u n ) xácđịnh bởi công thức truy hồi  u 1   =   2 u n + 1   =   u n   +   1 2   v ớ i   n ≥ 1 Chứng minh rằng có giới hạn hữu hạn khi Tìm giới hạn...
Đọc tiếp

Cho dãy số ( u n ) xácđịnh bởi công thức truy hồi  u 1   =   2 u n + 1   =   u n   +   1 2   v ớ i   n ≥ 1

Chứng minh rằng có giới hạn hữu hạn khi Tìm giới hạn đó.
#Toán lớp 11
1
CM
Cao Minh Tâm
14 tháng 3 2019

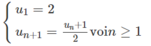
Giải sách bài tập Toán 11 | Giải sbt Toán 11

Ta có

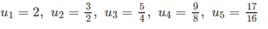
Giải sách bài tập Toán 11 | Giải sbt Toán 11

Dự đoán

Giải sách bài tập Toán 11 | Giải sbt Toán 11

Chứng minh dự đoán trên bằng quy nạp (bạn đọc tự chứng minh).

Từ đó

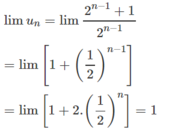
Giải sách bài tập Toán 11 | Giải sbt Toán 11

Đúng(0)
PT
Pham Trong Bach
22 tháng 8 2019
Cho dãy số u n  được xác định bởi  u 1 = 2 u n + 1 = 4 u n + 9 Dãy số v n  xác định bởi v n = u n + 3 , với mọi n ≥ 1 . Khẳng định nào dưới đây đúng?  A. Dãy  v n  là cấp số cộng với công sai d=3 . B. Dãy  ...
Đọc tiếp

Cho dãy số u n  được xác định bởi  u 1 = 2 u n + 1 = 4 u n + 9

Dãy số v n  xác định bởi v n = u n + 3 , với mọi n ≥ 1 . Khẳng định nào dưới đây đúng? 

A. Dãy  v n  là cấp số cộng với công sai d=3 .

B. Dãy  v n  là cấp số nhân với công bội q=4.

C. Dãy  v n  là cấp số cộng với công sai d=4 .

D. Dãy  v n  là cấp số nhân với công bội q= 9
#Toán lớp 11
1
CM
Cao Minh Tâm
22 tháng 8 2019

Đáp án B

Đúng(0)
PT
Pham Trong Bach
23 tháng 5 2019
Cho dãy số u n  được xác định bởi u 1 = 1 ; u n + 1 = 1 2 u n + 2 u n  với mọi n ≥ 1 . Tìm lim  u n A. 1 B. -1 C.  2 D. - 2 ...
Đọc tiếp

Cho dãy số u n  được xác định bởi u 1 = 1 ; u n + 1 = 1 2 u n + 2 u n  với mọi n ≥ 1 . Tìm lim  u n

A. 1

B. -1

C.  2

D. - 2

#Toán lớp 11
1
CM
Cao Minh Tâm
23 tháng 5 2019

Đúng(0)
MN
Minh Nguyệt
28 tháng 3 2021

Cho dãy số (un) được xác định như sau: u1= 2017; un-1= n2(un-1 - un) với mọi n ∈ N*, n ≥2. Tìm giới hạn dãy số (un)
#Toán lớp 11
1
AH
Akai Haruma
Giáo viên
28 tháng 3 2021

Lời giải:

$\frac{u_{n-1}}{u_n}=\frac{n^2}{n^2-1}>0$ với mọi $n\geq 2$ nên $u_{n-1}, u_n$ luôn cùng dấu.

Mà $u_1=2017>0$ nên $u_n>0$ với mọi $n=1,2,...$

Mặt khác:

$n^2(u_{n-1}-u_n)=u_{n-1}>0\Rightarrow u_{n-1}>u_n$ nên dãy $(u_n)$ là dãy giảm.

Dãy giảm và bị chặn dưới nên $u_n$ hội tụ. Đặt $\lim u_n=a$. 

Ta có: $a=n^2(a-a)\Rightarrow a=0$

Vậy $\lim u_n=0$

 

Đúng(0)
PT
Pham Trong Bach
1 tháng 9 2018
Cho dãy số có giới hạn (un) xác định bởi : u 1 = 1 2 u n + 1 = 1 2 - u n ,   n ≥ 1 . Tìm kết quả đúng của u n . A. 0. B. 1. C. -1. D. 1 2 ...
Đọc tiếp

Cho dãy số có giới hạn (un) xác định bởi : u 1 = 1 2 u n + 1 = 1 2 - u n ,   n ≥ 1 . Tìm kết quả đúng của u n .

A. 0.

B. 1.

C. -1.

D. 1 2 .
#Toán lớp 11
1
CM
Cao Minh Tâm
1 tháng 9 2018

Đúng(0)
PT
Pham Trong Bach
4 tháng 9 2018
Cho dãy số có giới hạn ( u n )  xác định bởi : u 1 = 1 2 u n + 1 = 1 2 - u n , n ≥ 1 . Tìm kết quả đúng của lim u n . A. 0. B. 1. C. -1. D. 1 2 ...
Đọc tiếp

Cho dãy số có giới hạn ( u n )  xác định bởi : u 1 = 1 2 u n + 1 = 1 2 - u n , n ≥ 1 . Tìm kết quả đúng của lim u n .

A. 0.

B. 1.

C. -1.

D. 1 2 .
#Toán lớp 11
1
CM
Cao Minh Tâm
4 tháng 9 2018

Đúng(0)
PT
Pham Trong Bach
12 tháng 1 2017
Xét dãy số (un), n ∈ N *  được xác định bởi hệ thức u 1 = 2 u n + 1 = 2 + u n . Tìm u10. A. u 10 = 2 cos π 2 11 B.  u 10 = 2 sin π 2 11 C.   u 10 = 2 cos ...
Đọc tiếp

Xét dãy số (un), n ∈ N *  được xác định bởi hệ thức u 1 = 2 u n + 1 = 2 + u n . Tìm u10.

A. u 10 = 2 cos π 2 11

B.  u 10 = 2 sin π 2 11

C.   u 10 = 2 cos π 2 10

D.  u 10 = 2 sin π 2 10

#Toán lớp 11
1
CM
Cao Minh Tâm
12 tháng 1 2017

Đáp án A

Chỉ ra được

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP