Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Ta có u n là cấp số nhân công bội bằng 2.
Ta có
2 4 u 1 + 1 + 2 3 - 2 u 2 = 2 4 u 1 + 1 + 2 3 - 4 u 1 ≥ 2 2 4 u 1 + 1 . 2 3 - 4 u 1 = 8
Mặt khác
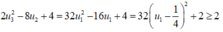
Suy ra
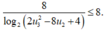
Vậy 2 4 u 1 + 1 + 2 3 - 2 u 2 = 8 log 2 ( 2 u 3 2 - 8 u 2 + 4 )
![]()
![]()
![]()
suy ra giá trị nhỏ nhất của n cần tìm là 2021

Chọn C
Phương pháp: Dễ thấy u n = u n - 1 + 6 , ∀ n ≥ 2 suy ra dãy số đã cho là cấp số cộng công sai bằng 6.
Vậy ta cần tìm số hạng đầu.
Cách giải: Ta có
log 2 u 5 + log 2 u 9 + 8 = 11
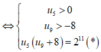
![]()
![]()
V ậ y u 1 = u 5 - 4 . 6 = 8
Do đó:
S n = u 1 + u 2 + . . + u n
= n u 1 + n ( n - 1 ) 2 d
= 3 n 2 + 5 n
⇔ 3 n 2 + 5 n - 32 > 0
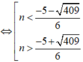
Vậy số tự nhiên n nhỏ nhất thỏa mãn S n ≥ 2 5 là 3.

Phương pháp:
Ứng với mỗi giá trị của n = 1, n = 2 ta tính các giá trị u2, u3 rồi tính giá trị của biểu thức.
Cách giải:
Ta có:
u n + 1 = u n + n , u 1 = 3
![]()
Chọn B

Chọn A.
Trước hết ta chứng minh 1 < un < 4
Điều này hiển nhiên đúng với n = 1.
Giả sử 1 < un < 4, ta có: ![]()
Ta chứng minh (un) là dãy tăng
Ta có u1 < u2, giả sử un-1 < un, ∀ n ≤ k.
Khi đó: 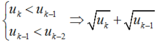
![]()
Vậy dãy (un) là dãy tăng và bị chặn.

\(u_n=2u_{n-1}+3n-1\)
\(\Leftrightarrow u_n+3n+5=2\left(u_{n-1}+3\left(n-1\right)+5\right)\)
Đặt \(u_n+3n+5=v_n\Rightarrow\left\{{}\begin{matrix}v_1=10\\v_n=2v_{n-1}\end{matrix}\right.\)
\(\Rightarrow v_n\) là CSN với công bội 2
\(\Rightarrow v_n=10.2^{n-1}\Rightarrow u_n+3n+5=10.2^{n-1}\)
\(\Leftrightarrow u_n=10.2^{n-1}-3n-5\)
\(\Rightarrow u_{2019}=10.2^{2018}+3.2019-1=...\)

a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = n^2 - 1:
u1 = 1^2 - 1 = 0 u2 = 2^2 - 1 = 3 u3 = 3^2 - 1 = 8 u4 = 4^2 - 1 = 15
Vậy u1 = 0, u2 = 3, u3 = 8, u4 = 15.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 99, ta giải phương trình n^2 - 1 = 99:
n^2 - 1 = 99 n^2 = 100 n = 10 hoặc n = -10
Vì số hạng của dãy phải là số tự nhiên nên ta chọn n = 10. Vậy số hạng thứ mấy có giá trị 99 là u10.
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = (2n - 1)/(n + 1):u1 = (21 - 1)/(1 + 1) = 1/2 u2 = (22 - 1)/(2 + 1) = 3/3 = 1 u3 = (23 - 1)/(3 + 1) = 5/4 u4 = (24 - 1)/(4 + 1) = 7/5
Vậy u1 = 1/2, u2 = 1, u3 = 5/4, u4 = 7/5.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 137137, ta giải phương trình (2n - 1)/(n + 1) = 137137:
(2n - 1)/(n + 1) = 137137 2n - 1 = 137137(n + 1) 2n - 1 = 137137n + 137137 137135n = 137138 n = 1
Vậy số hạng thứ mấy có giá trị 137137 là u1.
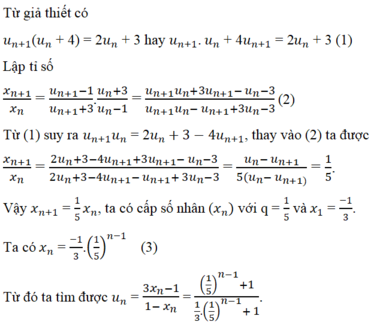


Chọn D.
Ta có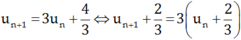
Đặt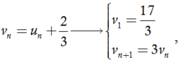
suy ra (vn) là cấp số nhân với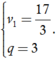
Suy ra u1 + u2 + … + un = (v1 + v2 + … + vn) – n.2/3
Yêu cầu bài toán:
Vậy giá trị nhỏ nhất của n thỏa mãn bài toán là n = 146.