Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có DE//BC
nên AD/AB=AE/AC
=>AE/4=1/3
hay AE=4/3(cm)
b: Xét ΔABC có DE//BC
nên AD/AB=AE/AC
hay \(AD\cdot AC=AE\cdot AB\)

Tự vẽ hình.
a) Xét tam giác OAB có AB // CD
⇒AOOC=OBOD=ABDC⇒12OC=93=18DC⇒AOOC=OBOD=ABDC⇒12OC=93=18DC ( Hệ quả định lý Ta - lét ) (1)
=> OC = 4cm, DC = 6cm
Vậy OC = 4cm và DC = 6cm
b) Xét tam giác FAB có DC // AB
⇒FDAD=FCCB⇒FD.BC=FC.AD⇒FDAD=FCCB⇒FD.BC=FC.AD ( ĐPCM )
c) Theo (1), ta đã có:
OAOC=OBOD⇒OAOA+OC=OBOB+OD⇒OAAC=OBBDOAOC=OBOD⇒OAOA+OC=OBOB+OD⇒OAAC=OBBD (2)
Vì MN // AB mà AB // DC => MN // DC
Xét tam giác ADC có MO// DC
⇒MODC=AOAC⇒MODC=AOAC ( Hệ quả định lý Ta - lét ) (3)
CMTT : ONDC=OBDBONDC=OBDB (4)
Từ (2), (3) và (4) => MODC=NODC⇒MO=NOMODC=NODC⇒MO=NO ( ĐPCM )

a: Xét ΔABC có DE//BC
nên AD/AB=DE/BC
=>DE/10=3/5
hay DE=6(cm)
b: Xét ΔADE và ΔCGE có
\(\widehat{ADE}=\widehat{CGE}\)
\(\widehat{AED}=\widehat{CEG}\)
Do đó: ΔADE\(\sim\)ΔCGE
Suy ra: AD/CG=AE/CE
hay \(AD\cdot CE=AE\cdot CG\)

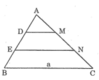
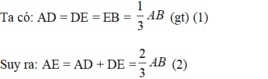
Trong ΔABC, ta có: DM // BC (gt)
Nên ![]() (Hệ quả định lí Ta-lét)
(Hệ quả định lí Ta-lét)
Suy ra : ![]() (3)
(3)
Từ (1) và (3) suy ra: 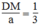
Suy ra: ![]()
Trong ΔABC, ta có: EN // BC (gt)
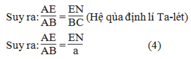
Từ (2) và (4) suy ra: 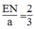 hay
hay 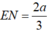

a: Xét ΔABC có DE//BC
nên DE/BC=AD/AB
=>DE/10=3/5
=>DE=6cm
b: Xét ΔADE và ΔCGE có
góc AED=góc CEG
góc EAD=góc ECG
=>ΔADE đồng dạng với ΔCGE
c: Xét tứ giác DBCG có
DG//BC
DB//CG
=>DBCG là hình bình hành
=>DB=CG

Bài 6 :
Tự vẽ hình nhá :)
a) Gọi O là giao điểm của AC và EF
Xét tam giác ADC có :
EO // DC => AE/AD = AO/AC (1)
Xét tam giác ABC có :
OF // DC
=> CF/CB = CO/CA (2)
Từ (1) và (2) => AE/AD + CF/CB = AO/AC + CO/CA = AO + CO/AC = AC/AC = 1 => đpcm
Bài 7 :
a) Do EF // AB => CF / CA = EF / AB => CF / EF = AC / AB (1)
Dựng MG // AC và M là trung điểm của cạnh BC => GM là đường trung bình của tam giác ABC => G là trung điểm của cạnh AB =>AG = BG
Do DK // GM => AD / AG = DK / GM => AD / BG = DK / GM
=> DK / AD = GM / BG = \(\frac{\frac{AC}{2}}{\frac{AB}{2}}=\frac{AC}{AB} \left(2\right)\)
Từ (1) và (2) => CF / EF = DK / AD
Mà tứ giác ADEF là hình bình hành ( vì EF // AD và DE // AF ) nên AD = È
=> CF = DK ( đpcm )
Bài 8 :
Ta có : AB = AM + MB = 11 + 8 = 19 ( cm )
Áp dụng hệ quả định lí Ta-lét vào tam giác ABC, ta có :
AM / AB = AN / AC => AM + AB / AB = AN + AC / AC => 19 + 11 / 19 = AN + 38 / 38 => 30/19 = 38 + AN / 38
=> 1140 = 19.AN + 722
=> AN = ( 1140 - 722 ) / 19 = 22 ( cm )
=> NC = 38 - 12 = 26 ( cm )

a: AE/AB=3/15=1/5
AD/AC=4/20=1/5
Do đó: AE/AB=AD/AC
b: Xét ΔADE và ΔACB có
AD/AC=AE/AB
góc A chung
Do đó: ΔADE\(\sim\)ΔACB
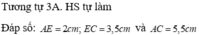
a: Xét ΔABC có DE//BC
nên AD/AB=AE/AC
=>AE/4=1/3
hay AE=4/3(cm)
b: Xét ΔABC có DE//BC
nên AD/AB=AE/AC
hay \(AD\cdot AC=AE\cdot AB\)