Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Gọi A là biến cố lấy ra hai đường chéo có giao điểm nằm trong đường tròn (C)
Số đường chéo của đa giác đều 20 đỉnh là
C
20
2
- 20 = 170. Khi đó, ta có số cách lấy ra 2 đường chéo trong số 170 đường là ![]()
Để có hai đường chéo cắt nhau tại một điểm nằm trong đường tròn (C) thì hai đường chéo đó phải là đường chéo của tứ giác có 4 đỉnh là đỉnh của đa giác đều 20 đỉnh. Do đó, số cách lấy ra 2 đường chéo có giao điểm nằm trong đường tròn tâm O là C 20 4 = 4845
Vậy xác suất lấy ra hai đường chéo có giao điểm nằm trong đường tròn (C) là
![]()

Chọn B
Các số tự nhiên của tập X có dạng a b c d e ¯ , suy ra tập X có 9. 10 4 số. Lấy từ tập X ngẫu nhiên hai số có C 90000 2 số.
Vì ![]()
![]() có 25 số.
có 25 số.
Suy ra số tự nhiên có năm chữ số chia hết cho 4 là 9.10.10.25 = 22500 số.
Số tự nhiên có năm chữ số không chia hết cho 4 là 9.10.10.75 = 67500 số.
Vậy xác suất để ít nhất một số chia hết cho 4 là: 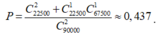

Đáp án C

Gọi A là biến cố: “Chọn được tam giác vuông”
Đa giác đều 4n đỉnh nội tiếp trong đường tròn tâm O có 2n đường chéo qua tâm O .
Mỗi tam giác vuông tạo bởi hai đỉnh nằm trên cùng một đường chéo qua tâm O và một đỉnh trong 4 n - 2 đỉnh còn lại.
Suy ra số tam giác vuông được tạo thành là C 2 n 1 . C 4 n - 2 1 .
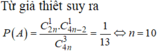

Đáp án A
Số các tam giác bất kỳ là n ( ω ) = C 18 3
Số các tam giác đều là 18 3 = 6
Có 18 các chọn một đỉnh của đa giác, mỗi đỉnh có 8 các chọn 2 đỉnh còn lại để được một tam giác đều
Số các tam giác cân là: 18.8 = 144
Số các tam giác cân không đều là: 144 - 6 = 138 => n(A) = 138
Xác suất => P(A) = 138 C 18 3 = 23 136

Chọn B
Gọi A là biến cố lấy ra hai đường chéo có giao điểm nằm trong đường tròn (C)
Số đường chéo của đa giác đều 20 đỉnh là
C
20
2
- 20 = 170. Khi đó, ta có số cách lấy ra 2 đường chéo trong số 170 đường là ![]()
Để có hai đường chéo cắt nhau tại một điểm nằm trong đường tròn (C) thì hai đường chéo đó phải là đường chéo của tứ giác có 4 đỉnh là đỉnh của đa giác đều 20 đỉnh. Do đó, số cách lấy ra 2 đường chéo có giao điểm nằm trong đường tròn tâm O là C 20 4 = 4845
Vậy xác suất lấy ra hai đường chéo có giao điểm nằm trong đường tròn (C) là
![]()

Chọn 3 đỉnh bất kỳ: \(n\left(\Omega\right)=C^3_n\left(cach\right)\)
Gọi 3 đỉnh đó là A,B,C tạo thành tam giác tù =>A >90 độ => B,C<90 độ
Chọn một đỉnh là B (hoặc C): \(C^1_n=n\left(cach\right)\)
Kẻ đường kính ua B chia đường tròn thành 2 nữa, mỗi nữa sẽ có \(\dfrac{n}{2}-1\) (đỉnh của đa giác đều)
Để tạo thành tam giác tù thì A và C (hoặc A và B) phải ở cùng một nữa
Số cách chọn A và C (A và B): \(C^2_{\dfrac{n}{2}-1}+C^2_{\dfrac{n}{2}-1}\left(cach\right)\)
\(\Rightarrow n\left(A\right)=\dfrac{1}{2}.n\left(C^2_{\dfrac{n}{2}-1}+C^2_{\dfrac{n}{2}-1}\right)\left(tam-giac-tu\right)\)
\(\Rightarrow p\left(A\right)=\dfrac{n\left(A\right)}{n(\Omega)}=...\)
Làm bừa xem đúng ko :D

SỐ tam giác tạo được từ 3 đỉnh là \(C^3_{12}\)
Số tam giác có 3 đỉnh là 3 đỉnh của đa giác và 2 cạnh là cạnh của đa giác: cứ 3 đỉnh liên tiếp cho 1 tam giác thỏa mãn
=>Có 12 tam giác
Số tam giác có 3 đỉnh là đỉnh của đa giác và 1 cạnh là cạnh của đa giác
=>CÓ 8*12=96 tam giác
=>\(P=\dfrac{C^3_{12}-12-12\cdot8}{C^3_{12}}\)

Đáp án C
Chọn ngẫu nhiên 4 đỉnh của đa giác có C 20 4 = 4845 c á c h
Đa giác đều 20 đỉnh có 10 đường chéo đi qua tâm đường tròn ngoại tiếp đa giác
Cứ 2 đường chéo bất kì là 2 đường chéo cuiả 1 hình chữ nhật
Do đó số hình chứ nhật là C 20 2 = 45
Vậy xác suất cần tìm là
P = 45 4845 = 3 323


Chọn D
Số phần tử của (S) là số đường thẳng tạo nên từ 30 điểm đã cho là C 30 2 = 435
Số cách chọn 2 đường thẳng bất kỳ thuộc tập (S) là số phần tử không gian mẫu n ( Ω ) = C 435 2 = 94395
Giao điểm của hai đường thẳng nằm trong đường tròn tức là cũng nằm ở miền trong đa giác 30 đỉnh, khi đó giao điểm 2 đường thẳng cũng là giao điểm hai đường chéo của tứ giác có 4 đỉnh thuộc 30 đỉnh đa giác đã cho, vậy số giao điểm nằm trong đa giác chính là C 30 4 = 27405
Vậy xác suất cần tìm là