Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{FAC}\) chung
Do đó: ΔAEB∼ΔAFC(g-g)

a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
góc BAE chung
=>ΔABE đồng dạng với ΔACF
b: Xét ΔHFB vuông tại F và ΔHEC vuông tại E có
góc FHB=góc EHC
=>ΔHFB đồng dạng với ΔHEC
=>HF/HE=HB/HC
=>HF*HC=HB*HE

a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
góc A chung
=>ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE*AC=AB*AF và AE/AB=AF/AC
b: Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc A chung
=>ΔAEF đồng dạng với ΔABC

a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
\(\widehat{BAH}\) chung
Do đó: ΔABH\(\sim\)ΔACK
b: Xét ΔKEB vuông tại K và ΔHEC vuông tại H có
\(\widehat{KEB}=\widehat{HEC}\)
DO đó: ΔKEB\(\sim\)ΔHEC
Suy ra: EK/EH=EB/EC
hay \(\dfrac{EK}{EB}=\dfrac{EH}{EC}\)
c: Xét ΔAKH và ΔACB có
AK/AC=AH/AB
góc A chung
Do đó: ΔAKH\(\sim\)ΔACB
Suy ra: \(\widehat{AKH}=\widehat{ACB}\)
 CHÚC BẠN HỌC TỐT
CHÚC BẠN HỌC TỐT





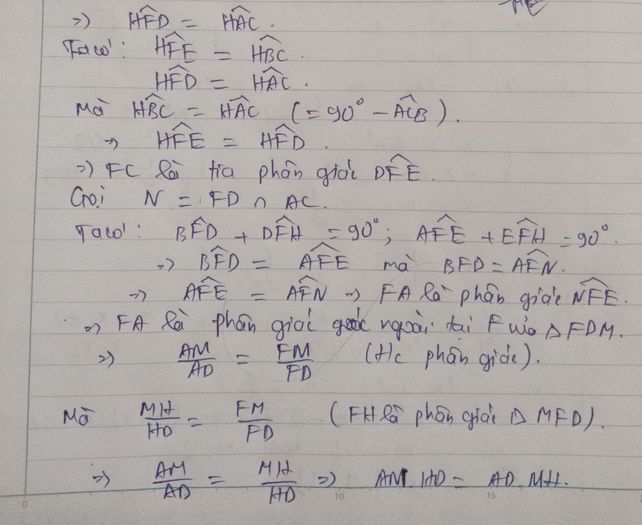 Bạn tham khảo cách làm nhé!
Bạn tham khảo cách làm nhé!


\(a,\left\{{}\begin{matrix}\widehat{AKH}=\widehat{HMC}\left(=90\right)\\\widehat{AHK}=\widehat{MHC}\left(đối.đỉnh\right)\end{matrix}\right.\Rightarrow\Delta AHK\sim\Delta CHM\left(g.g\right)\)
\(b,\left\{{}\begin{matrix}\widehat{AKC}=\widehat{ANB}\left(=90\right)\\\widehat{BAC}.chung\end{matrix}\right.\Rightarrow\Delta AKC\sim\Delta ANB\left(g.g\right)\\ \Rightarrow\dfrac{AN}{AK}=\dfrac{AB}{AC}\)
\(c,\left\{{}\begin{matrix}\widehat{HAN}+\widehat{AHN}=90;\widehat{BHM}+\widehat{HBM}=90\\\widehat{AHN}=\widehat{BHM}\left(đối.đỉnh\right)\end{matrix}\right.\Rightarrow\widehat{HAN}=\widehat{HBM}\)
\(\left\{{}\begin{matrix}\widehat{BMA}=\widehat{AMC}\left(=90\right)\\\widehat{HBM}=\widehat{HAN}\end{matrix}\right.\Rightarrow\Delta BHM\sim\Delta ACM\left(g.g\right)\Rightarrow\dfrac{MH}{CM}=\dfrac{MB}{MA}\Rightarrow MH\cdot MA=MB\cdot MC\)